Object Detection
In this context, object detection refers to the localization of the circle, rectangle and triangle on an image with the use of bounding boxes. Classification refers to identification of object colors, namely red, green and blue.
RetinaNet uses resNet as the model’s backbone. I have selected a small resNet, resNet 18. The details of the implementation can be found in the code below. The outputs of the resNet are three feature maps of different spatial resolutions, denoted by the white rectangles with gray boarders on the left (see the figure from the original publication below, Focal Loss for Dense Object Detection).
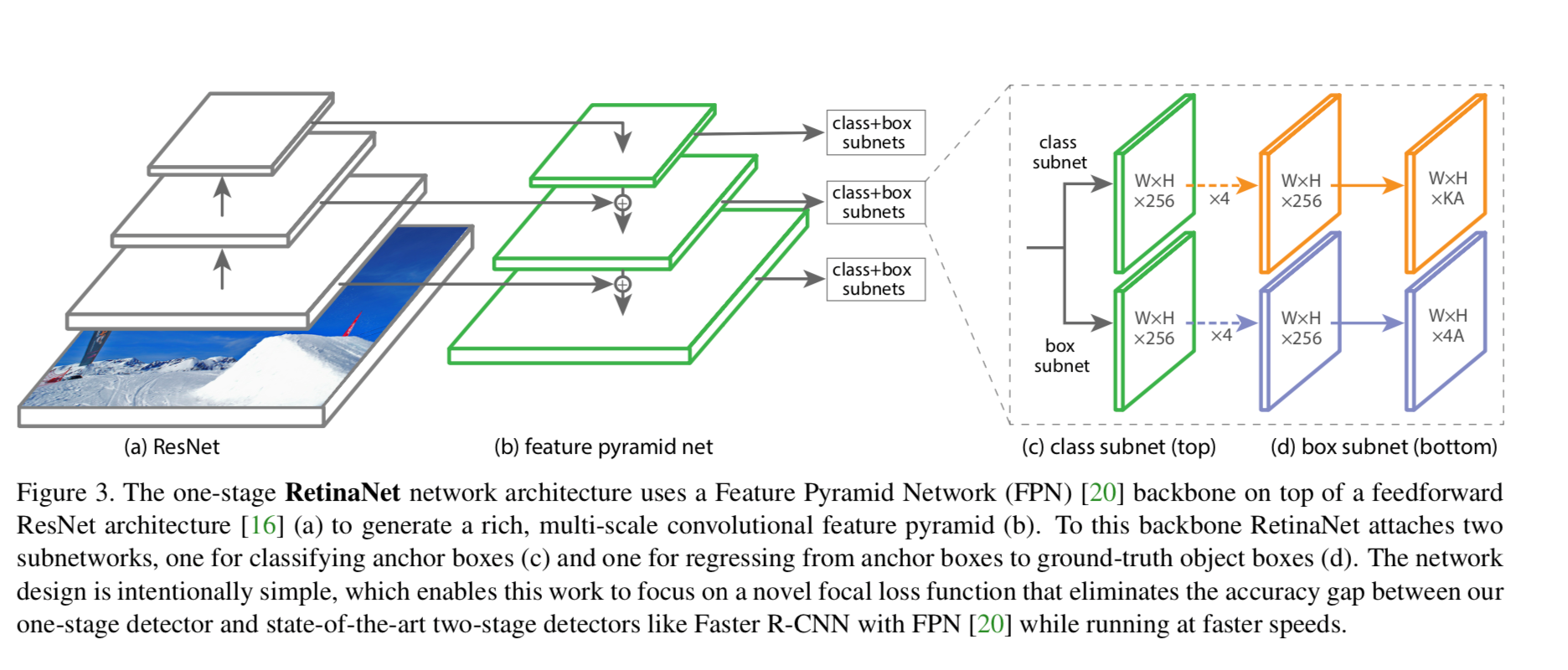
These feature maps are fed into a feature pyramid net (in green) which extends the hierarchical scales of spatial resolutions from three to five. One way to visualize the feature pyramid is to look at the green pyramid in the figure below. Note that resolution increases as we move down, and vice versa. This concept is particularly important because these scales help ensure the network can detect objects of various sizes as they appear across the scales. For example, a person may appear quite big in a portrait but tiny in a busy traffic scene as one amongst many pedestrians.
class PyramidFeatures(nn.Module):
def __init__(self, C3_size, C4_size, C5_size, feature_size=256):
super(PyramidFeatures, self).__init__()
# upsample C5 to get P5 from the FPN paper
self.P5_1 = nn.Conv2d(C5_size, feature_size, kernel_size=1, stride=1, padding=0)
self.P5_upsampled = nn.Upsample(scale_factor=2, mode='nearest')
self.P5_2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, stride=1, padding=1)
# add P5 elementwise to C4
self.P4_1 = nn.Conv2d(C4_size, feature_size, kernel_size=1, stride=1, padding=0)
self.P4_upsampled = nn.Upsample(scale_factor=2, mode='nearest')
self.P4_2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, stride=1, padding=1)
# add P4 elementwise to C3
self.P3_1 = nn.Conv2d(C3_size, feature_size, kernel_size=1, stride=1, padding=0)
self.P3_2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, stride=1, padding=1)
# "P6 is obtained via a 3x3 stride-2 conv on C5"
self.P6 = nn.Conv2d(C5_size, feature_size, kernel_size=3, stride=2, padding=1)
# "P7 is computed by applying ReLU followed by a 3x3 stride-2 conv on P6"
self.P7_1 = nn.ReLU()
self.P7_2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, stride=2, padding=1)
def forward(self, inputs):
C3, C4, C5 = inputs
P5_x = self.P5_1(C5)
P5_upsampled_x = self.P5_upsampled(P5_x)
P5_x = self.P5_2(P5_x)
P4_x = self.P4_1(C4)
P4_x = P5_upsampled_x + P4_x
P4_upsampled_x = self.P4_upsampled(P4_x)
P4_x = self.P4_2(P4_x)
P3_x = self.P3_1(C3)
P3_x = P3_x + P4_upsampled_x
P3_x = self.P3_2(P3_x)
P6_x = self.P6(C5)
P7_x = self.P7_1(P6_x)
P7_x = self.P7_2(P7_x)
return [P3_x, P4_x, P5_x, P6_x, P7_x]
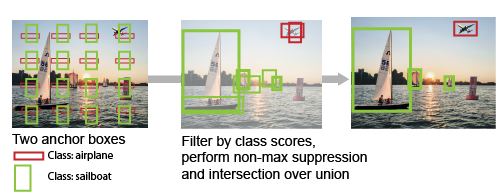
One of the most important ideas is that objects can appear anywhere. To detect them successfully, we need to scan the entire image evenly. To do so, we cover an image with pre-defined regions (anchor boxes) that break up the entire image. We can set the ratios and scales of these boxes such that they can capture objects of various sizes and shapes. The left-most diagram shows how anchor boxes systematically cover the entire image.
class Anchors(nn.Module):
def __init__(self, pyramid_levels=None, strides=None, sizes=None, ratios=None, scales=None):
super(Anchors, self).__init__()
if pyramid_levels is None:
self.pyramid_levels = [3, 4, 5, 6, 7]
if strides is None:
self.strides = [2 ** x for x in self.pyramid_levels]
if sizes is None:
self.sizes = [2 ** (x + 2) for x in self.pyramid_levels]
if ratios is None:
self.ratios = np.array([0.5, 1, 2])
if scales is None:
self.scales = np.array([2**-1.0, 2**-0.5, 2 ** 0, 2 ** (1.0 / 3.0), 2 ** (2.0 / 3.0)])
print ('-----Anchor boxes setting------')
print ('pyramid_levels {}'.format(self.pyramid_levels))
print ('strides {}'.format(self.strides))
print ('sizes {}'.format(self.sizes))
print ('ratios {}'.format(self.ratios))
print ('scales {}'.format(self.scales))
self.num_anchors = len(self.ratios) * len(self.scales)
print ('num_anchors {}'.format(self.num_anchors))
def forward(self, image):
image_shape = image.shape[2:]
image_shape = np.array(image_shape)
image_shapes = [(image_shape + 2 ** x - 1) // (2 ** x) for x in self.pyramid_levels]
# compute anchors over all pyramid levels
all_anchors = np.zeros((0, 4)).astype(TORCH_DATATYPE)
for idx, p in enumerate(self.pyramid_levels):
anchors = generate_anchors(base_size=self.sizes[idx], ratios=self.ratios, scales=self.scales)
shifted_anchors = shift(image_shapes[idx], self.strides[idx], anchors)
all_anchors = np.append(all_anchors, shifted_anchors, axis=0)
all_anchors = np.expand_dims(all_anchors, axis=0)
all_anchors = torch.from_numpy(all_anchors.astype(TORCH_DATATYPE))
if torch.cuda.is_available():
all_anchors = all_anchors.cuda()
return all_anchors
def generate_anchors(base_size=16, ratios=None, scales=None):
"""
Generate anchor (reference) windows by enumerating aspect ratios X
scales w.r.t. a reference window.
"""
if ratios is None:
ratios = np.array([0.5, 1, 2])
if scales is None:
scales = np.array([2 ** 0, 2 ** (1.0 / 3.0), 2 ** (2.0 / 3.0)])
num_anchors = len(ratios) * len(scales)
# initialize output anchors
anchors = np.zeros((num_anchors, 4))
# scale base_size
anchors[:, 2:] = base_size * np.tile(scales, (2, len(ratios))).T
# compute areas of anchors
areas = anchors[:, 2] * anchors[:, 3]
# correct for ratios
anchors[:, 2] = np.sqrt(areas / np.repeat(ratios, len(scales)))
anchors[:, 3] = anchors[:, 2] * np.repeat(ratios, len(scales))
# transform from (x_ctr, y_ctr, w, h) -> (x1, y1, x2, y2)
anchors[:, 0::2] -= np.tile(anchors[:, 2] * 0.5, (2, 1)).T
anchors[:, 1::2] -= np.tile(anchors[:, 3] * 0.5, (2, 1)).T
return anchors
def compute_shape(image_shape, pyramid_levels):
"""Compute shapes based on pyramid levels.
:param image_shape:
:param pyramid_levels:
:return:
"""
image_shape = np.array(image_shape[:2])
image_shapes = [(image_shape + 2 ** x - 1) // (2 ** x) for x in pyramid_levels]
return image_shapes
def anchors_for_shape(
image_shape,
pyramid_levels=None,
ratios=None,
scales=None,
strides=None,
sizes=None,
shapes_callback=None,
):
image_shapes = compute_shape(image_shape, pyramid_levels)
# compute anchors over all pyramid levels
all_anchors = np.zeros((0, 4))
for idx, p in enumerate(pyramid_levels):
anchors = generate_anchors(base_size=sizes[idx], ratios=ratios, scales=scales)
shifted_anchors = shift(image_shapes[idx], strides[idx], anchors)
all_anchors = np.append(all_anchors, shifted_anchors, axis=0)
return all_anchors
def shift(shape, stride, anchors):
shift_x = (np.arange(0, shape[1]) + 0.5) * stride
shift_y = (np.arange(0, shape[0]) + 0.5) * stride
shift_x, shift_y = np.meshgrid(shift_x, shift_y)
shifts = np.vstack((
shift_x.ravel(), shift_y.ravel(),
shift_x.ravel(), shift_y.ravel()
)).transpose()
# add A anchors (1, A, 4) to
# cell K shifts (K, 1, 4) to get
# shift anchors (K, A, 4)
# reshape to (K*A, 4) shifted anchors
A = anchors.shape[0]
K = shifts.shape[0]
all_anchors = (anchors.reshape((1, A, 4)) + shifts.reshape((1, K, 4)).transpose((1, 0, 2)))
all_anchors = all_anchors.reshape((K * A, 4))
return all_anchors
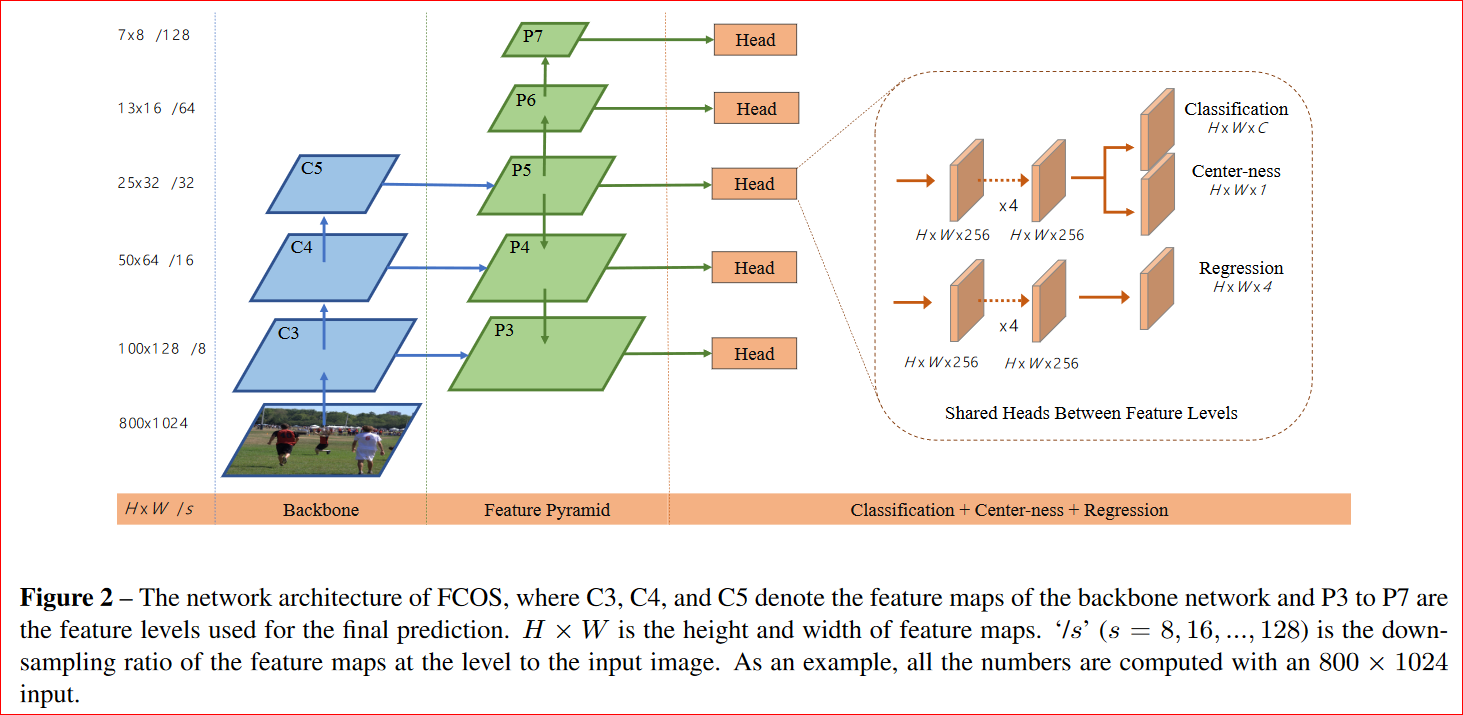
In this toy example, I have tried Ratios = [0.5, 1, 2], Scales = [0.5, 0.7, 1, 1.25, 1,6], totaling 15 combinations. A ratio of 1 is good for circle and square. By imposing a minimum area in the generation of the toy dataset, I make sure the samples are easy for the network because I do not need to look at scales that are below 0.5. But, what if a circle, triangle, or rectangle does not fall in these pre-determine box sizes? The solution to this is a class + box subnet branches.
The class + box subnet comprises of two independent branches. The class subnet branch (ClassificationModel) predicts the classes of the object, may it be circle, rectangle or triangle. K is the number of shapes. In this case, K is 3. A represents the number of pre-defined anchor boxes. The box subnet branch (RegressionModel)predicts how the pre-defined anchor boxes ought to be adjusted to fit the object tightly. It regresses the change needed to apply to the corners of the most relevant anchor boxes or those with a circle, triangle or rectangle inside (see diagram in the middle and far-right). Note that the class + box subnet’s weights are shared across all levels and locations.
class RegressionModel(nn.Module):
def __init__(self, num_features_in, num_anchors=9, feature_size=256):
super(RegressionModel, self).__init__()
self.conv1 = nn.Conv2d(num_features_in, feature_size, kernel_size=3, padding=1)
self.act1 = nn.ReLU()
self.conv2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act2 = nn.ReLU()
self.conv3 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act3 = nn.ReLU()
self.conv4 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act4 = nn.ReLU()
self.output = nn.Conv2d(feature_size, num_anchors * 4, kernel_size=3, padding=1)
def forward(self, x):
out = self.conv1(x)
out = self.act1(out)
out = self.conv2(out)
out = self.act2(out)
out = self.conv3(out)
out = self.act3(out)
out = self.conv4(out)
out = self.act4(out)
out = self.output(out)
# out is B x C x W x H, with C = 4*num_anchors
out = out.permute(0, 2, 3, 1)
return out.contiguous().view(out.shape[0], -1, 4)
class ClassificationModel(nn.Module):
def __init__(self, num_features_in, num_anchors=9, num_classes=80, prior=0.01, feature_size=256):
super(ClassificationModel, self).__init__()
self.num_classes = num_classes
self.num_anchors = num_anchors
self.conv1 = nn.Conv2d(num_features_in, feature_size, kernel_size=3, padding=1)
self.act1 = nn.ReLU()
self.conv2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act2 = nn.ReLU()
self.conv3 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act3 = nn.ReLU()
self.conv4 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=1)
self.act4 = nn.ReLU()
self.output = nn.Conv2d(feature_size, num_anchors * num_classes, kernel_size=3, padding=1)
self.output_act = nn.Sigmoid()
def forward(self, x):
out = self.conv1(x)
out = self.act1(out)
out = self.conv2(out)
out = self.act2(out)
out = self.conv3(out)
out = self.act3(out)
out = self.conv4(out)
out = self.act4(out)
out = self.output(out)
out = self.output_act(out)
# out is B x C x W x H, with C = n_classes + n_anchors
out1 = out.permute(0, 2, 3, 1)
batch_size, width, height, channels = out1.shape
out2 = out1.view(batch_size, width, height, self.num_anchors, self.num_classes)
return out2.contiguous().view(x.shape[0], -1, self.num_classes)
When we interpret the network’s classification and detected bounding boxes, we need to decide which detected boxes are chosen to represent the detected object. In other words, when multiple anchor boxes overlap (measured by intersection-over-union) with each other for a single object to a greater or lesser degree, we choose the box with the highest classification scores and with good overlaps among competing detected boxes. Such situation calls for non-maximum suppression algorithm. The threshold in this model is 0.5 (standard).
transformed_anchors = self.regressBoxes(anchors, regression)
transformed_anchors = self.clipBoxes(transformed_anchors, img_batch)
finalResult = [[], [], []]
finalScores = torch.Tensor([])
finalAnchorBoxesIndexes = torch.Tensor([]).long()
finalAnchorBoxesCoordinates = torch.Tensor([])
if torch.cuda.is_available():
finalScores = finalScores.cuda()
finalAnchorBoxesIndexes = finalAnchorBoxesIndexes.cuda()
finalAnchorBoxesCoordinates = finalAnchorBoxesCoordinates.cuda()
for i in range(classification.shape[2]):
scores = torch.squeeze(classification[:, :, i])
scores_over_thresh = (scores > 0.05)
if scores_over_thresh.sum() == 0:
# no boxes to NMS, just continue
continue
scores = scores[scores_over_thresh]
anchorBoxes = torch.squeeze(transformed_anchors)
anchorBoxes = anchorBoxes[scores_over_thresh]
# post-processing non-maximum suppression
anchors_nms_idx = nms(anchorBoxes, scores, 0.5)
finalResult[0].extend(scores[anchors_nms_idx])
finalResult[1].extend(torch.tensor([i] * anchors_nms_idx.shape[0]))
finalResult[2].extend(anchorBoxes[anchors_nms_idx])
finalScores = torch.cat((finalScores, scores[anchors_nms_idx]))
# control the number of predicted classes, one for each box
finalAnchorBoxesIndexesValue = torch.tensor([i] * anchors_nms_idx.shape[0])
if torch.cuda.is_available():
finalAnchorBoxesIndexesValue = finalAnchorBoxesIndexesValue.cuda()
finalAnchorBoxesIndexes = torch.cat((finalAnchorBoxesIndexes, finalAnchorBoxesIndexesValue))
finalAnchorBoxesCoordinates = torch.cat((finalAnchorBoxesCoordinates, anchorBoxes[anchors_nms_idx]))
Below, I have draw the computational graph of the RetinaNet. However, it is far to complicated to really draw the steps taken inside the network, but I show you the graph anyway. 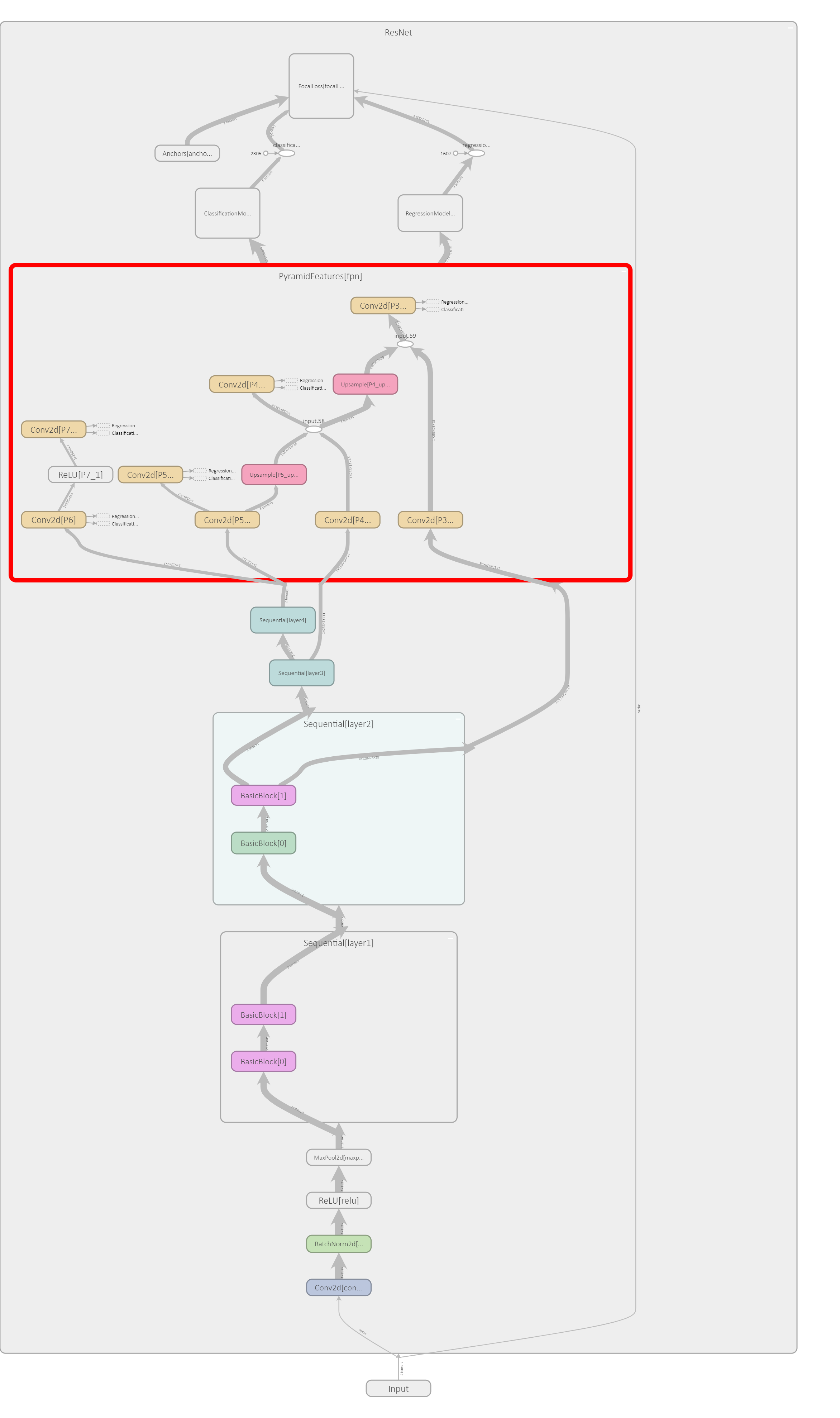
TensorboardX can keep track of the computations being done throughout the network as long as the inputs and outputs are pytorch tensors. That means I have only drawn the parts from input up to right after class + box subnets and focal loss operation. Thus, I draw the computational graph by doing the followings:
import os
from tensorboardX import SummaryWriter
from model_retinaNet import resnet18
writer = SummaryWriter(logdir=logdir, flush_secs=2)
alpha = 0.25
gamma = 2.0
model = resnet18(num_classes = 3, alpha, gamma)
model.eval() # not training
model.cuda() # on gpu
model.calculate_focalLoss = False
dummy_input = torch.rand(1,3,224,224).cuda() # random input on gpu
'''
very important to note that
1) the input must be tensor
2) write can only keep track of tensor, not native python objects.
this becomes problematic when the model transforms anchor boxes
'''
write.add_graph(model, input_to_model=dummy_input,
verbose=True)
writer.close()
Focal Loss
Given the size of the canvas versus the number of objects, we can tell that a vast majority of the anchor boxes do not contain anything and therefore are irrelevant. This imbalance overwhelms network learning with too many easy negative examples. One trick to make training possible is to reduce the weight of the loss on negative samples. Focal loss is one way to achieve this. The basic component of focal loss is binary cross entropy loss, but focal loss uses an extra factor (1-p) ^exponent and alpha to control the contribution of well-classified and less well-classified examples in the loss. As the gamma / exponent rises, the contribution of loss from well-classified examples shrinks.
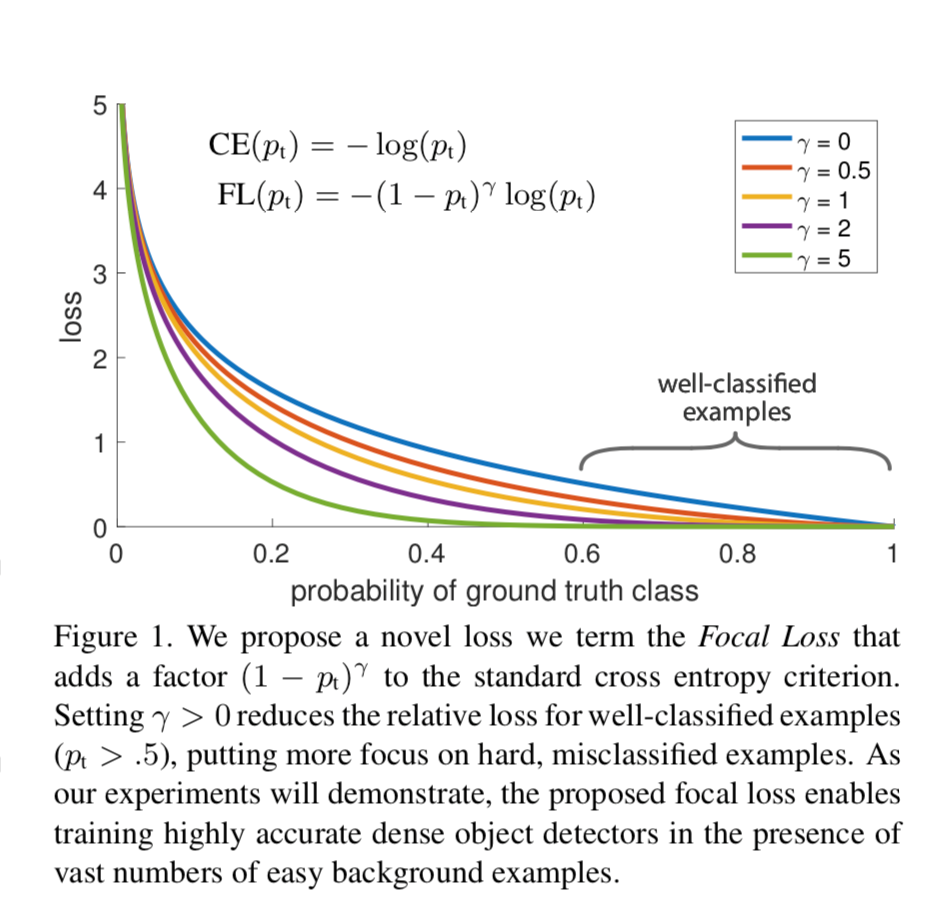
With this knowledge, here is the implementation of a small RetinaNet for detecting circles, rectangles and triangles.
class FocalLoss(nn.Module):
def __init__(self, alpha, gamma):
super(FocalLoss, self).__init__()
self.alpha = alpha
self.gamma = gamma
def forward(self, classifications, regressions, anchors, annotations):
batch_size = classifications.shape[0]
classification_losses = []
regression_losses = []
anchor = anchors[0, :, :]
anchor_widths = anchor[:, 2] - anchor[:, 0]
anchor_heights = anchor[:, 3] - anchor[:, 1]
anchor_ctr_x = anchor[:, 0] + 0.5 * anchor_widths
anchor_ctr_y = anchor[:, 1] + 0.5 * anchor_heights
for j in range(batch_size):
classification = classifications[j, :, :]
regression = regressions[j, :, :]
bbox_annotation = annotations[j, :, :]
bbox_annotation = bbox_annotation[bbox_annotation[:, 4] != -1]
# prevent issues with log, cannot be too close to 0 or 1
classification = torch.clamp(classification, 1e-4, 1.0 - 1e-4)
'''
calculate focal loss
'''
'''
special case : no object per image
'''
if bbox_annotation.shape[0] == 0:
alpha_factor = torch.ones(classification.shape)* self.alpha
alpha_factor = place_on_cpu_gpu(alpha_factor)
alpha_factor = 1. - alpha_factor
focal_weight = classification
focal_weight = alpha_factor * torch.pow(focal_weight, self.gamma)
bce = -(torch.log(1.0 - classification))
IoU = calc_iou(anchors[0, :, :], bbox_annotation[:, :4]) # num_anchors x num_annotations
IoU_max, IoU_argmax = torch.max(IoU, dim=1) # num_anchors x 1
#import pdb
#pdb.set_trace()
# compute the loss for classification
targets = torch.ones(classification.shape) * -1
targets = place_on_cpu_gpu(targets)
# create a one-hot-like encoding by simple thresholding
targets[torch.lt(IoU_max, 0.4), :] = 0
positive_indices = torch.ge(IoU_max, 0.5)
num_positive_anchors = positive_indices.sum()
assigned_annotations = bbox_annotation[IoU_argmax, :]
targets[positive_indices, :] = 0
targets[positive_indices, assigned_annotations[positive_indices, 4].long()] = 1
alpha_factor = torch.ones(targets.shape) * self.alpha
alpha_factor = place_on_cpu_gpu(alpha_factor)
alpha_factor = torch.where(torch.eq(targets, 1.), alpha_factor, 1. - alpha_factor)
focal_weight = torch.where(torch.eq(targets, 1.), 1. - classification, classification)
focal_weight = alpha_factor * torch.pow(focal_weight, self.gamma)
bce = -(targets * torch.log(classification) + (1.0 - targets) * torch.log(1.0 - classification))
# cls_loss = focal_weight * torch.pow(bce, gamma)
cls_loss = focal_weight * bce
zero_holder = torch.zeros(cls_loss.shape)
zero_holder = place_on_cpu_gpu(zero_holder)
cls_loss = torch.where(torch.ne(targets, -1.0), cls_loss, zero_holder)
cls_loss = place_on_cpu_gpu(cls_loss)
# avoid division by zero error
classification_losses.append(cls_loss.sum()/torch.clamp(num_positive_anchors.float(), min=1.0))
# compute the loss for regression
if positive_indices.sum() > 0:
assigned_annotations = assigned_annotations[positive_indices, :]
anchor_widths_pi = anchor_widths[positive_indices]
anchor_heights_pi = anchor_heights[positive_indices]
anchor_ctr_x_pi = anchor_ctr_x[positive_indices]
anchor_ctr_y_pi = anchor_ctr_y[positive_indices]
gt_widths = assigned_annotations[:, 2] - assigned_annotations[:, 0]
gt_heights = assigned_annotations[:, 3] - assigned_annotations[:, 1]
gt_ctr_x = assigned_annotations[:, 0] + 0.5 * gt_widths
gt_ctr_y = assigned_annotations[:, 1] + 0.5 * gt_heights
# clip widths to 1
gt_widths = torch.clamp(gt_widths, min=1)
gt_heights = torch.clamp(gt_heights, min=1)
targets_dx = (gt_ctr_x - anchor_ctr_x_pi) / anchor_widths_pi
targets_dy = (gt_ctr_y - anchor_ctr_y_pi) / anchor_heights_pi
targets_dw = torch.log(gt_widths / anchor_widths_pi)
targets_dh = torch.log(gt_heights / anchor_heights_pi)
targets = torch.stack((targets_dx, targets_dy, targets_dw, targets_dh))
targets = targets.t()
targets = place_on_cpu_gpu(targets)
targets_scale = torch.Tensor([[0.1, 0.1, 0.2, 0.2]])
targets_scale = place_on_cpu_gpu(targets_scale)
# negative_indices = 1 + (~positive_indices)
regression_diff = torch.abs(targets - regression[positive_indices, :])
# squared error
# torch where is like an if statement, if true then A otherwise B
regression_loss = torch.where(
torch.le(regression_diff, 1.0 / 9.0),
0.5 * 9.0 * torch.pow(regression_diff, 2),
regression_diff - 0.5 / 9.0
)
regression_losses.append(regression_loss.mean())
else:
regression_loss = torch.tensor(0).float()
regression_loss = place_on_cpu_gpu(regression_loss)
regression_losses.append(regression_loss)
return torch.stack(classification_losses), torch.stack(regression_losses)
Color Classification
Since we are trying to also identify the color of the shapes, I construct a color classifier based on convolutional neural network with a few layers. Technically, RGB channels provide the exact color information and therefore multi-layer network is really not called for. Nonetheless, it is interesting to see that the network generalizes very well and does not show any sign of over fitting (more about this later in the result section). Below, I have draw the computational graph of the color classification network. Because the color classifier is nothing more than a few cascading blocks with a convolutional layer + batch norm + non-linearity layer (ReLU) + max pooling, the graph looks very neat.
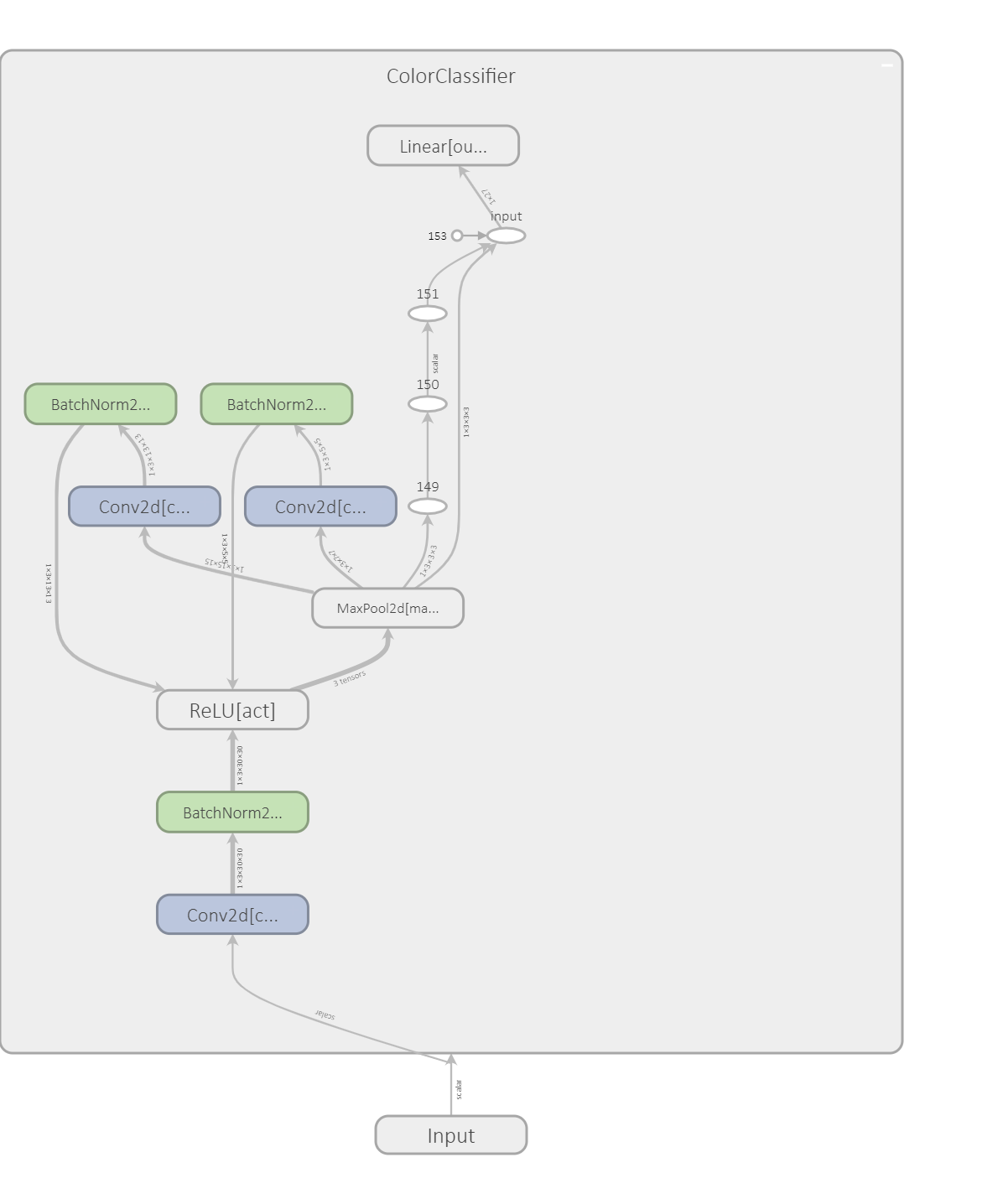
class ColorClassifier(nn.Module):
def __init__(self, feature_size, num_features_in=3, num_classes=80):
super(ColorClassifier, self).__init__()
self.num_classes = num_classes
self.act = nn.ReLU(inplace=True)
self.conv1 = nn.Conv2d(num_features_in, feature_size, kernel_size=3, padding=0)
self.bn1 = nn.BatchNorm2d(feature_size)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.conv2 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=0)
self.bn2 = nn.BatchNorm2d(feature_size)
self.conv3 = nn.Conv2d(feature_size, feature_size, kernel_size=3, padding=0)
self.bn3 = nn.BatchNorm2d(feature_size)
self.output = nn.Linear(3*3*3, num_classes)
def forward(self, x):
out = self.conv1(x)
out = self.bn1(out)
out = self.act(out)
out = self.maxpool(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.act(out)
out = self.maxpool(out)
out = self.conv3(out)
out = self.bn3(out)
out = self.act(out)
out = self.maxpool(out)
out = out.view(out.size(0), -1)
out = self.output(out)
return out
Please feel free to play around with the code in my repository.
Reference
Parts of the code are adapted from the following resources:
- https://lilianweng.github.io/lil-log/2018/12/27/object-detection-part-4.html
- https://www.jeremyjordan.me/object-detection-one-stage/
- https://github.com/signatrix/efficientdet
- http://pjreddie.com/yolo9000/
- https://github.com/yhenon/pytorch-retinanet
