Introduction
This three-part series aims to teach readers how to create a web application that configures, solves, and displays the minimization of Rosenbrock function by Differential Evolution algorithm and L-BFGS algorithm. Such application is very useful for anyone who wishes to monitor the step-by-step progress of the minimization. A gradual fall in the energy or function value is a good sign and the opposite is a bad sign. Early signs help to suggest how appropriate the initial guesses or bounds might be. For instance, overly tight bounds or far off guesses usually makes the optimizer oscillate or stagnate at sub-optimal solutions. This is especially paramount for image registration because its objective function (numerical similarity metric) may only correlate partially to how human discern visual similarity.
In Part I, I describe how to modify the existing Scipy functions (namely Differential Evolution algorithm and L-BFGS algorithm) so that we can obtain the step-by-step or intermediate solutions. I also explain why the built-in callback option is not viable for us when the code runs on the server.
In Part II, I describe how to create a web page that represents our graphical user interface that interacts with the server in Part III. While differential evolution algorithm requires no gradient approximation, L-BFGS estimates first order function derivatives (which are then linearly combined to approximate its second order derivatives). The web page layout must therefore adapt to the outputs of the algorithms, and its content must be updated dynamically via streaming. To achieve this, I describe how I make use of Template.
In Part III, I describe how to use Flask (micro-framework) to make a very basic server that parses user’s request, calls the correct Scipy routines to minimize Rosenbrock function, and renders a complete set of solutions in HTML.
Prerequisites
- Python 3.10
- Flask 2.2.2
- Scipy 1.9.3
- Numpy 1.23.5
- Windows 10
Part I - Scipy Optimization Functions
We can conveniently locate many commonly used optimization algorithms (wrapped in Python) in Scipy library. Amongst them, I have modified differential evolution algorithm and L-BFGS algorithm. Since differential evolution algorithm does not require the estimation of objective function gradients, we can try it out on problems that do not offer a quick calculation of gradients. However, the gradient often indicates the direction in which a better solution may reside. L-BFGS takes the gradient into account when updating the current estimate of a solution.
I let Rosenbrock function, which is commonly featured in toy examples, be the objective function. Coefficient a and coefficient b determine the shape of the valley of the function.
def rosenbrock_func(a,b,x):
"""
x is a 1-D vector (N,)
"""
return (a-x[0])**2.0 + b*((x[1]-x[0]**2.0)**2.0)
The differential evolution solver in Scipy package is the full implementation of the differential evolution algorithm. What I need to modify is to make it suitable for streaming on the server. So I create a class called ModifiedEvolution that inherits DifferentialEvolutionSolver.
On a Flask server, streaming is implemented as a generator object. As the generator yields its information that arrives piece-by-piece, the piece is sent to client directly (in a form of a Flask response object).
With that methodology in mind, ModifiedEvolution has three sequential methods, namely initialize_population, evolving, and polishing. The initialize_population creates a population of possible solution at the beginning. The evolving is a generator that streams or yields all intermediate steps of a solution. The polishing polishes the solution found by differential evolution by L-BFGS algorithm and gives us back a typical Scipy optimization result object.
# https://github.com/scipy/scipy/blob/v1.10.0/scipy/optimize/_differentialevolution.py#L22-L399
class ModifiedEvolution(DifferentialEvolutionSolver):
def __init__(self, func, bounds, args=(),
strategy='best1bin',
maxiter=1000, popsize=15, tol=0.01,
mutation=(0.5, 1), recombination=0.7, seed=None,
callback=None, disp=False, polish=True,
init='latinhypercube', atol=0, updating='immediate',
workers=1, constraints=(), x0=None, *,
integrality=None, vectorized=False):
super().__init__(func, bounds, args=args,
strategy=strategy,
maxiter=maxiter,
popsize=popsize, tol=tol,
mutation=mutation,
recombination=recombination,
seed=seed, polish=polish,
callback=callback,
disp=disp, init=init, atol=atol,
updating=updating,
workers=workers,
constraints=constraints,
x0=x0,
integrality=integrality,
vectorized=vectorized)
# placeholder
self.warning_flag = False
self.status_message = None
self.last_nit = None
def initialize_population(self):
self.status_message = _status_message['success']
# The population may have just been initialized (all entries are
# np.inf). If it has you have to calculate the initial energies.
# Although this is also done in the evolve generator it's possible
# that someone can set maxiter=0, at which point we still want the
# initial energies to be calculated (the following loop isn't run).
if np.all(np.isinf(self.population_energies)):
self.feasible, self.constraint_violation = (
self._calculate_population_feasibilities(self.population))
# only work out population energies for feasible solutions
self.population_energies[self.feasible] = (
self._calculate_population_energies(
self.population[self.feasible]))
self._promote_lowest_energy()
def evolving(self):
# do the optimization.
for nit in range(1, self.maxiter + 1):
# evolve the population by a generation
try:
next(self) # I am a generator!
except StopIteration:
self.warning_flag = True
if self._nfev > self.maxfun:
self.status_message = _status_message['maxfev']
elif self._nfev == self.maxfun:
self.status_message = ('Maximum number of function evaluations'
' has been reached.')
break
if self.disp:
print(f"differential_evolution step {nit}: f({self.x})= {self.population_energies[0]}")
if self.callback:
c = self.tol / (self.convergence + _MACHEPS)
self.warning_flag = bool(self.callback(self.x, convergence=c))
if self.warning_flag:
self.status_message = ('callback function requested stop early'
' by returning True')
# should the solver terminate?
if self.warning_flag or self.converged():
break
yield (nit, self.x, self.population_energies[0])
# slow down for visualization
# time.sleep(1)
else:
self.status_message = _status_message['maxiter']
self.warning_flag = True
self.last_nit = nit
print ('reaching the end.................')
def package_results(self):
DE_result = OptimizeResult(
x=self.x,
fun=self.population_energies[0],
nfev=self._nfev,
nit=self.last_nit,
message=self.status_message,
success=(self.warning_flag is not True))
return DE_result
def perform_polishing(self):
DE_result = self.package_results()
if self.polish and not np.all(self.integrality):
DE_result = self.polishing(DE_result)
return DE_result
def polishing(self, DE_result, polish_method = 'L-BFGS-B'):
# can't polish if all the parameters are integers
if np.any(self.integrality):
# set the lower/upper bounds equal so that any integrality
# constraints work.
limits, integrality = self.limits, self.integrality
limits[0, integrality] = DE_result.x[integrality]
limits[1, integrality] = DE_result.x[integrality]
if self._wrapped_constraints:
polish_method = 'trust-constr'
constr_violation = self._constraint_violation_fn(DE_result.x)
if np.any(constr_violation > 0.):
warnings.warn("differential evolution didn't find a"
" solution satisfying the constraints,"
" attempting to polish from the least"
" infeasible solution", UserWarning)
if self.disp:
print(f"Polishing solution with '{polish_method}'")
result = minimize(self.func,
np.copy(DE_result.x),
method=polish_method,
bounds=self.limits.T,
constraints=self.constraints)
self._nfev += result.nfev
DE_result.nfev = self._nfev
# Polishing solution is only accepted if there is an improvement in
# cost function, the polishing was successful and the solution lies
# within the bounds.
if (result.fun < DE_result.fun and
result.success and
np.all(result.x <= self.limits[1]) and
np.all(self.limits[0] <= result.x)):
DE_result.fun = result.fun
DE_result.x = result.x
DE_result.jac = result.jac
# to keep internal state consistent
self.population_energies[0] = result.fun
self.population[0] = self._unscale_parameters(result.x)
if self._wrapped_constraints:
DE_result.constr = [c.violation(DE_result.x) for
c in self._wrapped_constraints]
DE_result.constr_violation = np.max(
np.concatenate(DE_result.constr))
DE_result.maxcv = DE_result.constr_violation
if DE_result.maxcv > 0:
# if the result is infeasible then success must be False
DE_result.success = False
DE_result.message = ("The solution does not satisfy the "
f"constraints, MAXCV = {DE_result.maxcv}")
return DE_result
Although Scipy implementation provides a callback option, I could not turn it into a generator-like object. If that were achievable, much less coding would be required.
ModifiedLBFGSB has three sequential methods, namely initialization, solving, and package_result. The initialization prepares variables in a way that are compatible with the Fortran L-FBGS code. The solving represents a generator-like object. The package_result gives the optimization result as in a typical Scipy optimization algorithm.
# from https://github.com/scipy/scipy/blob/dde50595862a4f9cede24b5d1c86935c30f1f88a/scipy/optimize/_lbfgsb_py.py#L386
class ModifiedLBFGSB:
def __init__(self, fun, x0, args=(), jac=None, bounds=None,
disp=None, maxcor=10, ftol=2.2204460492503131e-09,
gtol=1e-5, eps=1e-8, maxfun=15000, maxiter=15000,
iprint=-1, callback=None, maxls=20,
finite_diff_rel_step=None, **unknown_options):
_check_unknown_options(unknown_options)
self.m = maxcor
self.pgtol = gtol
self.factr = ftol / np.finfo(float).eps
self.callback = callback
self.maxfun = maxfun
self.maxiter = maxiter
x0 = asarray(x0).ravel()
self.n, = x0.shape
if bounds is None:
bounds = [(None, None)] * self.n
if len(bounds) != self.n:
print (bounds, self.n, x0)
raise ValueError('length of x0 != length of bounds')
# unbounded variables must use None, not +-inf, for optimizer to work properly
bounds = [(None if l == -np.inf else l, None if u == np.inf else u) for l, u in bounds]
# LBFGSB is sent 'old-style' bounds, 'new-style' bounds are required by
# approx_derivative and ScalarFunction
new_bounds = old_bound_to_new(bounds)
# check bounds
if (new_bounds[0] > new_bounds[1]).any():
raise ValueError("LBFGSB - one of the lower bounds is greater than an upper bound.")
# initial vector must lie within the bounds. Otherwise ScalarFunction and
# approx_derivative will cause problems
x0 = np.clip(x0, new_bounds[0], new_bounds[1])
self.iprint = True
sf = _prepare_scalar_function(fun, x0, jac=jac, args=args, epsilon=eps,
bounds=new_bounds,
finite_diff_rel_step=finite_diff_rel_step)
self.func_and_grad = sf.fun_and_grad
self.sf = sf
fortran_int = _lbfgsb.types.intvar.dtype
self.nbd = zeros(self.n, fortran_int)
self.low_bnd = zeros(self.n, float64)
self.upper_bnd = zeros(self.n, float64)
self.bounds_map = {(None, None): 0,
(1, None): 1,
(1, 1): 2,
(None, 1): 3}
for i in range(0, self.n):
l, u = bounds[i]
if l is not None:
self.low_bnd[i] = l
l = 1
if u is not None:
self.upper_bnd[i] = u
u = 1
self.nbd[i] = self.bounds_map[l, u]
if not maxls > 0:
raise ValueError('maxls must be positive.')
else:
self.maxls = maxls
self.x = array(x0, float64)
self.f = array(0.0, float64)
self.g = zeros((self.n,), float64)
self.wa = zeros(2*self.m*self.n + 5*self.n + 11*self.m*self.m + 8*self.m, float64)
self.iwa = zeros(3*self.n, fortran_int)
self.task = zeros(1, 'S60')
self.csave = zeros(1, 'S60')
self.lsave = zeros(4, fortran_int)
self.isave = zeros(44, fortran_int)
self.dsave = zeros(29, float64)
self.task[:] = 'START'
self.n_iterations = 0
def solving(self):
while 1:
# x, f, g, wa, iwa, task, csave, lsave, isave, dsave = \
_lbfgsb.setulb(self.m, self.x, self.low_bnd, self.upper_bnd, self.nbd, self.f, self.g, self.factr,
self.pgtol, self.wa, self.iwa, self.task, self.iprint, self.csave, self.lsave,
self.isave, self.dsave, self.maxls)
task_str = self.task.tobytes()
if task_str.startswith(b'FG'):
# The minimization routine wants f and g at the current x.
# Note that interruptions due to maxfun are postponed
# until the completion of the current minimization iteration.
# Overwrite f and g:
self.f, self.g = self.func_and_grad(self.x)
yield (self.n_iterations, self.x, self.sf.nfev,self.f,self.g)
elif task_str.startswith(b'NEW_X'):
# new iteration
self.n_iterations += 1
if self.callback is not None:
self.callback(np.copy(self.x))
if self.n_iterations >= self.maxiter:
self.task[:] = 'STOP: TOTAL NO. of ITERATIONS REACHED LIMIT'
elif self.sf.nfev > self.maxfun:
self.task[:] = ('STOP: TOTAL NO. of f AND g EVALUATIONS '
'EXCEEDS LIMIT')
# this step calculates the solution at the end of an iteration
# thus, we cannot see the steps taken to evaluate numerical gradient at f'(x)
# yield (self.n_iterations, self.x, self.sf.nfev,self.f,self.g)
else:
break
# print ('self.n_iterations {}, self.x {}, self.sf.nfev {}, f {}, g {}'.format(
# self.n_iterations,
# self.x,
# self.sf.nfev,
# self.f,
# self.g))
def package_result(self):
task_str = self.task.tobytes().strip(b'\x00').strip()
if task_str.startswith(b'CONV'):
warnflag = 0
elif self.sf.nfev > self.maxfun or self.n_iterations >= self.maxiter:
warnflag = 1
else:
warnflag = 2
# These two portions of the workspace are described in the mainlb
# subroutine in lbfgsb.f. See line 363.
s = self.wa[0: self.m*self.n].reshape(self.m, self.n)
y = self.wa[self.m*self.n: 2*self.m*self.n].reshape(self.m, self.n)
# See lbfgsb.f line 160 for this portion of the workspace.
# isave(31) = the total number of BFGS updates prior the current iteration;
n_bfgs_updates = self.isave[30]
n_corrs = min(n_bfgs_updates, self.m)
hess_inv = LbfgsInvHessProduct(s[:n_corrs], y[:n_corrs])
task_str = task_str.decode()
result = OptimizeResult(fun=self.f, jac=self.g, nfev=self.sf.nfev,
njev=self.sf.ngev,
nit=self.n_iterations, status=warnflag, message=task_str,
x=self.x, success=(warnflag == 0), hess_inv=hess_inv)
print (result)
return result
As an aside, I design these solver objects with compatibility in mind. Thus, they take in the same set of parameters and output the same OptimizeResult object as the original Scipy implementation.
Part II - Graphical User Interface / Web page
To understand the graphical user interface of the web application, let’s start by taking a closer look at the final web page.
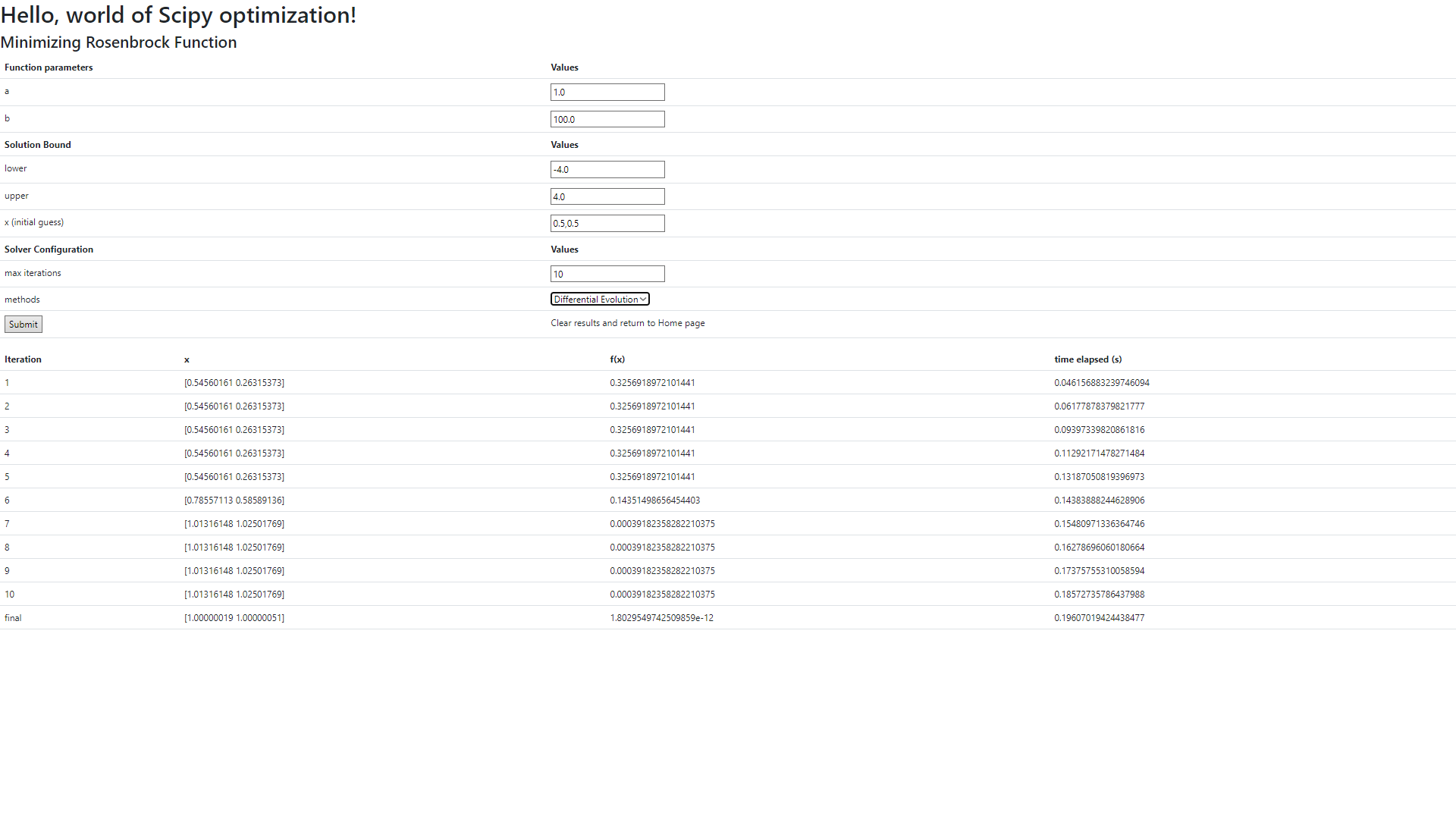
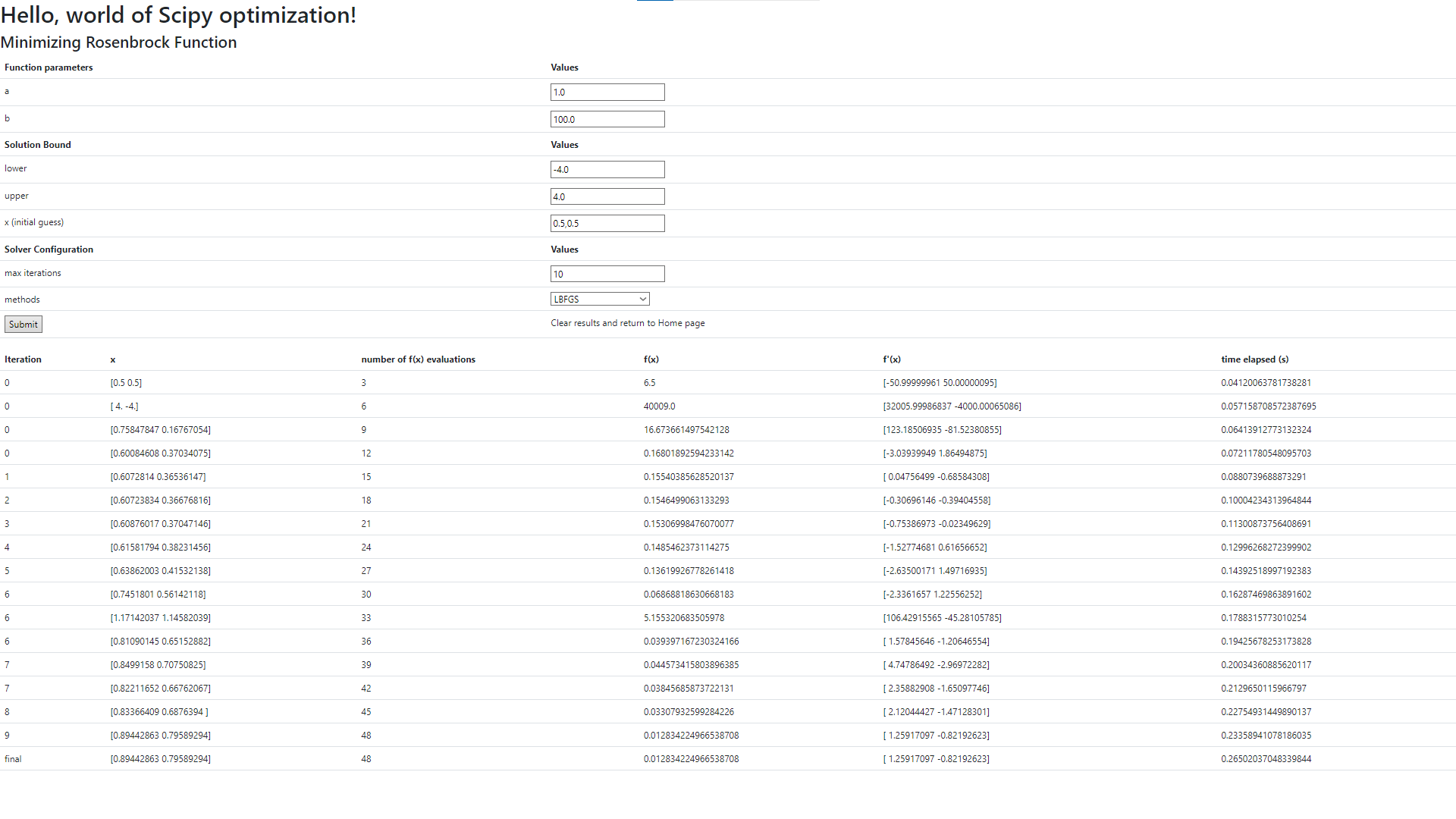
The upper half contains the configuration of the Rosenbrock function, solution space, and the optimization algorithms. (the Rosenbrock function coefficients, choice of the optimization algorithm, the upper and lower bounds of the search space, initial guesses of solution (x), and the maximum number of iterations) The lower half contains a table of the sequential steps of a chosen optimizer.
Bootstrap provides this basic design of the web page; Juxtapose allows users to visually compare the intermediate solutions of each algorithm. Pushing the central slider left or right reveals the screen-shot of the web page for differential evolution outputs and L-BFGS outputs respectively.
Even though the screen-shots are static, in reality, during streaming, the HTML of the web page is updated dynamically by the server responses. An easy way to achieve this is to manipulate HTML by Flask, which provides APIs that leverage Jinja2 engine that generate new HTML from HTML templates.
I have made heavy use of variables, if statements, for loops and filters in Jinja2. The form input variable values are set by Python string variables. Practically speaking, the default input values are python string that are hard coded on the server.
I need to take extra care when it comes to the result table headers. Unlike differential evolution algorithm, L-BFGS calculates the gradient of the objective function. Jinja2 length filter tells me how many items are sent back. I then know what names should go in the header!
Outer for loop creates HTML code snippets that renders the row of the intermediate result table; the inner for loop creates table data code snippet which populates the table row with values that are being streamed from server. The namespace variable allows me to turn off header after the first row.
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width, initial-scale=1">
<title>Scipy optimization demo</title>
<link href="https://cdn.jsdelivr.net/npm/bootstrap@5.2.3/dist/css/bootstrap.min.css" rel="stylesheet" integrity="sha384-rbsA2VBKQhggwzxH7pPCaAqO46MgnOM80zW1RWuH61DGLwZJEdK2Kadq2F9CUG65" crossorigin="anonymous">
</head>
<body>
<h1>Hello, world of Scipy optimization!</h1>
<h3>Minimizing Rosenbrock Function </h3>
<script src="https://cdn.jsdelivr.net/npm/bootstrap@5.2.3/dist/js/bootstrap.bundle.min.js" integrity="sha384-kenU1KFdBIe4zVF0s0G1M5b4hcpxyD9F7jL+jjXkk+Q2h455rYXK/7HAuoJl+0I4" crossorigin="anonymous"></script>
<form action="/solver" method="post">
<table class="table">
<thead>
<tr>
<th> Function parameters</th>
<th> Values</th>
</tr>
</thead>
<tbody>
<tr>
<td>a</td>
<td><input type="text" id="a" name="a" value={{a}}></td>
</tr>
<tr>
<td>b</td>
<td><input type="text" id="b" name="b" value={{b}}></td>
</tr>
</tbody>
<thead>
<tr>
<th> Solution Bound</th>
<th> Values</th>
</thead>
<tbody>
<tr>
<td>lower</td>
<td><input type="text" id="lower" name="lower" value={{lower}}></td>
</tr>
<tr>
<td>upper</td>
<td><input type="text" id="upper" name="upper" value={{upper}}></td>
</tr>
<tr>
<td>x (initial guess)</td>
<td><input type="text" id="initialGuess" name="initialGuess" value={{initialGuess}}></td>
</tr>
</tbody>
<thead>
<tr>
<th> Solver Configuration</th>
<th> Values</th>
</tr>
</thead>
<tbody>
<tr>
<td>max iterations</td>
<td><input type="text" id="maxiter" name="maxiter" value={{maxiter}}></td>
</tr>
<tr>
<td>methods</td>
<td>
<select id="methods" name="methods">
<option value="LBFGS">LBFGS</option>
<option value="Differential Evolution">Differential Evolution</option>
</select>
</td>
</tr>
</tbody>
<tr>
<td><input type="submit"></td>
<td><a class="nav-link" href="{{ url_for('hello_world') }}">Clear results and return to Home page</a></td>
</tr>
</tbody>
</table>
</form>
<!--
namespace ensures the variable is available outside of this scope (including the for loop) !
--->
{% set display = namespace(header=true) %}
{% for (result, timeElapsed) in results %}
{% if display.header %}
<table class="table">
{% if result | length == 3 %}
<thead>
<tr>
<th> Iteration</th>
<th> x </th>
<th> f(x) </th>
<th> time elapsed (s) </th>
</tr>
</thead>
{% elif result | length == 5 %}
<thead>
<tr>
<th> Iteration</th>
<th> x </th>
<th> number of f(x) evaluations</th>
<th> f(x) </th>
<th> f'(x) </th>
<th> time elapsed (s) </th>
</tr>
</thead>
{% endif %}
<tbody>
{% set display.header = false %}
{% endif %}
<tr>
{% for item in result %}
<td> {{item}} </td>
{% endfor %}
<td> {{timeElapsed}} </td>
</tr>
{% endfor %}
</tbody>
</table>
</body>
</html>
Part III - Flask Server
Flask is my first choice for setting up a web server (WSGI - web server gateway interface application) because its documentation is quite comprehensive and its APIs are quite readable. The reason is seven-fold.
- Flask manages the endpoints using a decorator
- Flask handles request via a request object and response via a response object for you
- Flask renders HTML template automatically
- Flask isolates the current application scope and lets programmers create variables or default values inside it
- String variables are easily passed around
- Flask has default settings, a feature that simplifies the code (i.e. all HTML templates are placed under templates folder, a location where Flask goes to and looks up templates files automatically)
- By running flask run –reload –debugger in the command prompt, reload means Flask detects file change and reloads the latest version; debugger shows an error traceback on the HTML page
To show you what the project structure is like, I draw a tree using windows tree /f command. This organization helps reduce the risk of circular importing.
C:.
│ run_app.py
│
├───api
│ │ routes.py
│ │ scipyOptimizer.py
│ │ __init__.py
│ │
│ ├───templates
│ │ callback.html
│ │
│ └───__pycache__
│ routes.cpython-310.pyc
│ scipyOptimizer.cpython-310.pyc
│ __init__.cpython-310.pyc
│
└───__pycache__
run_app.cpython-310.pyc
The server starts when Flask runs run_app.py. I often set Flask environment variable before calling flask run for the sake of convenience. (use Set FLASK_APP=run_app.py on windows)
from api import app
if __name__ == "__main__":
app.run(debug=True)
The api module initializes the application as shown below:
from flask import Flask
from flask import current_app, render_template, stream_template, Response, request
app = Flask(__name__)
app.debug=True
with app.app_context():
"""
Default optimization setting
"""
current_app.a = 1.0
current_app.b = 100.0
current_app.lower = -4.0
current_app.upper = 4.0
current_app.maxiter = 10
current_app.initialGuess = "0.5,0.5"
from api import routes
Note that we must initialize all routes. Or else we cannot find our endpoints.
The routes are listed below:
from flask import current_app, render_template, stream_template, Response, request
from .scipyOptimizer import ModifiedEvolution, rosenbrock_func, ModifiedLBFGSB
import time, os
import numpy as np
from functools import partial
from api import app
def extract_form(request):
# we cannot get json as we did not submit json >_<
# variable_name = request.get_json()
#
a = request.form.get('a')
b = request.form.get('b')
lower = request.form.get('lower')
upper = request.form.get('upper')
maxiter = request.form.get('maxiter')
initialGuess = request.form.get('initialGuess')
print ('initialGuess ', initialGuess)
initialGuess = [float(value) for value in initialGuess.split(',')]
# values in request objects are string
func = partial(rosenbrock_func, float(a), float(b))
maxiter = int(maxiter)
lower = float(lower)
upper = float(upper)
bounds = [(lower,upper), (lower,upper)]
print ('bounds ', bounds)
return bounds, maxiter, initialGuess, func, a, b, lower, upper
@app.route('/')
def hello_world():
return render_template("callback.html", maxiter=current_app.maxiter,
a=current_app.a,
b=current_app.b,
lower=current_app.lower,
upper=current_app.upper,
initialGuess=current_app.initialGuess)
@app.route("/solver", methods=['POST'])
def solver():
methods = request.form.get('methods')
print ('methods = ', methods)
if methods == "Differential Evolution":
return callEvolution()
elif methods == "LBFGS":
return call_LBFGS()
else:
raise RuntimeError('unknown methods')
@app.route("/evolve", methods=["POST"])
def callEvolution():
bounds, maxiter, initialGuess, func, a, b, lower, upper = extract_form(request)
# start a timer to see how long it takes to solve the problem
start_time = time.time()
def add_html():
"""
Create a generator that produces the intermediate results of the optimizer
"""
# using a context manager means that any created Pool objects are
# cleared up.
# don't pass args because they try to enter the f(x) as arguments
with ModifiedEvolution(func, bounds, maxiter=maxiter,
polish=True, disp=True) as solver:
solver.initialize_population()
for intermediate_results in solver.evolving():
yield (intermediate_results, time.time()-start_time)
result = solver.perform_polishing()
yield (("final", result.x, result.fun), time.time()-start_time)
return Response(stream_template('callback.html',
results=add_html(),
initialGuess=','.join([str(i) for i in initialGuess]),
maxiter=maxiter, a=a, b=b,
lower=lower, upper=upper))
@app.route('/lbfgs', methods=['POST'])
def call_LBFGS():
bounds, maxiter, initialGuess, func, a, b, lower, upper = extract_form(request)
# start a timer to see how long it takes to solve the problem
start_time = time.time()
solver = ModifiedLBFGSB(func, initialGuess, maxiter=maxiter, bounds=bounds)
def add_html(solver):
"""
Create a generator that produces the intermediate results of the optimizer
"""
for intermediate_results in solver.solving():
yield (intermediate_results, time.time()-start_time)
result = solver.package_result()
yield (("final", result.x, result.nfev, result.fun, result.jac), time.time()-start_time)
return Response(stream_template('callback.html',
results=add_html(solver),
initialGuess=','.join([str(i) for i in initialGuess]),
maxiter=maxiter, a=a, b=b,
lower=lower, upper=upper))
I always extract user’s form to obtain the most up-to-date configurations. When Flask renders the HTML page, I pass the configurations along so that the user configurations are persistent (without being overwritten by default optimization setting) on the HTML page. It is worth noting that stream_with_context can also be used here if the request object ought to be retained during streaming.
