Introduction
I spent a total of several months to read a book called “Algorithms to live by: The computer science of human decisions” written by Brian Christian and Tom Griffiths. The book shows us why algorithmic thinking not only is useful for computer scientists but also is helpful to laymen. Concise writing and elegant explanation, the book reveals insights from decades of research in computer science that, in principle, can be applied to our everyday lives to solve common decision-making problems and illuminate the workings of the human mind.
Our lives are constrained by a set amount of space, resources and time, limits that give rise to a particular set of problems and force us to choose among alternatives and to not have them all. How to do so efficiently and effectively has been central to computer science.
What should we do, or leave undone, in a day or a lifetime? How much messiness should we accept? What is the cost of messiness? What balance of new activities and familiar favorites is the most fulfilling?
The book succinctly illustrates how the problems in computer science mirror the problems in daily living. The book starts from the basic concepts such as sorting and moves to the more advanced such as networks, from man vs nature to man vs society. Thus, its content is well-suited for all ages with different backgrounds.
Man vs nature, man vs self
- Enough is enough (chapter1: Optimal stopping : when to stop looking),
- Trade off between exploration and exploitation (chapter2: Explore/exploit : the familiar vs. the greatest)
- In what order and what comes first (chapter3: Sorting : making order)
- What to forget (chapter4: Caching : forget about it)
- Timing is everything (chapter5: Scheduling : first thing first)
- When should we change our mind (chapter6: Bayes’s Rule : predicting the future)
- Thinking becomes harmful (chapter7: Overfitting : when to think less)
- Time to compromise (chapter8: Relaxation : let it slide)
- Roll the dice (chapter9: Randomness : when to leave it to chance)
Man vs society
- We are in this together (chapter10: Networking : how we connect)
- Play games (chapter11: Game theory : the minds of others)
Personally, out of all the chapters, I enjoy the chapter on optimal stopping the most. Optimal stopping is the most intriguing of all, for life is of finite length with an uncertain end date.
If you read the recommendations found on book stores such as Amazon or somewhere else of that sort, you will find that many readers would recommend this book because of the insights computer scientists have to offer. While I agree with their recommendations, I think it is also paramount to take note that the level of details in the book is insufficient to truly teach someone to start thinking and behaving like a computer scientist. At best, the descriptions are introduction to some elementary principles or concepts widely adopted or even taken for granted by the computer science community today. With that being said, for me, when I read this book, I can learn to apply the theories outside of the classroom.
Chapter 1
Optimal stopping tries to solve the problem of when we should stop searching optimally and make a decision under resource constraints such as time. The best way to illustrate optimal stopping is via the infamous secretory problem. The secretory problem is a challenge on hiring the best candidate among all the applicants for a secretory role.
Once the job advertisement has been posted, we’ve in total received N applicants. The total number of applicants are of paramount to this problem. The more applicants, the harder it is to find the best amongst them unless we use the method described in the book.
These applicants are interviewed in the order of their application submission dates, from the earliest to the latest. We rank each applicant by his or her performance during an interview. This implies that we do not know anything about the performance of applicants who have yet to be interviewed. Thus, all the information that is available to make the hiring decision only stems from the past, nothing from the future.
To make the story is bit more interesting, the book introduces the element of a seller’s market. In a seller’s market, if we offer an applicant a job, he or she is assumed to accept our offer on the spot. However, if an offer is not given right away, the applicant is gone forever. Therefore, at the end of each interview, we either offer a job or reject an applicant immediately.
The aim of the secretory problem is to hire the best candidate from a pool of applicants.
In mathematical modelling, we assume that the order these applicants submit the applications is random. In other words, the best applicant could appear at any position of the interview waiting list. In this problem, our baseline method is to offer one of the applicants the job randomly without an interview. If the total number of applicants is N, the chances for us to have hired the best applicants is 1/N. As N increases, our probability of success shrinks EXPONENTIALLY.
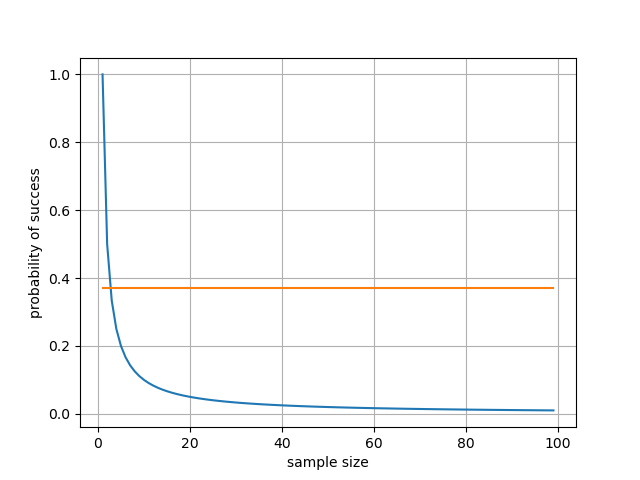
Now we know our baseline performance. Can we do better than the baseline performance?
The authors suggest a “look-and-leap” approach with 37% rule. The rule strikes an optimal balance between knowing the distribution of candidate quality and having enough chances to offer a job to “the-best-seen-so-far” candidate.
One caveat we must highlight is that in this optimal stopping challenge, by its very definition of the goal, says that we should never never hire someone who is worse than the best we have ever seen. However, as we shall see in later chapters of the book such behaviour may be warranted when we take other factors into considerations.
What makes the secretary problem hard is that the more time we spend on interviewing applicants, our “best-seen-so-far” persona is going to improve. Meanwhile, we are becoming less likely to encounter someone better than the “best-seen-so-far”. That means we have already missed out on the best applicant. Therefore, we must make a trade off between the proportion of applicants that is used to sample the underlying distribution, the look phase, and the proportion of applicants that is used to wait for the “best-seen-so-far”, the leap phase.
Specifically, the look phase requires us to interview and rank applicants from the “worst-seen-so-far” to the “best-seen-so-far”. The look phase takes up 37% of the entire pool of applicants. Hence, the name 37% rule. After the look phase in which we have identified our “best-seen-so-far” persona, we enter the leap phase. Since we have rejected every applicant in the look phase, we must accept one applicant in the leap phase. The rule of acceptance is that this applicant ought to be better than the “best-seen-so-far” in look phase.
Even with this look-and-then-leap strategy, the probability of success is only 37%. In other words, 63% chance of not locating the best applicant. However, one advantage of this look-and-then-leap strategy offers is that the strategy can be scaled up- its probability of success is independent of sample size, N. Thus, as N increases (mathematically speaking whenever N is greater than 3), the more we should employ this look-and-then-leap strategy.
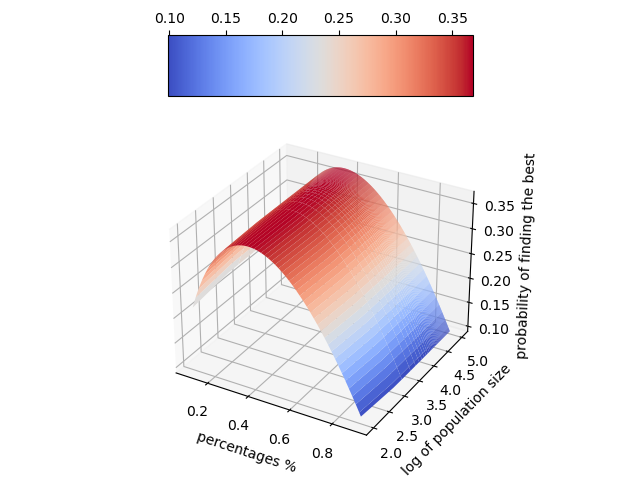
Can we reduce our effort and time spend in the look phase to improve the overall efficiency of the strategy?
The answer is a resounding YES. However, we must obtain our information regarding the quality of applicants in a form of distributions from other reliable sources, including but not limited to population census, standardized examinations such as an SAT score, etc.
If we modify our secretary problem slightly (say we instead of hire 1 applicant, we hire h applicants), our challenge is shifted from hiring the best to hiring h good-enough applicants.
Here I explore two simple distributions, namely Gaussian and uniform distributions. Apart from being easy to compute, I choose Gaussian and uniform distributions, for they often represent real-world distributions. For example, the height of the population roughly follows a Gaussian distribution. For those who expect their future spouse to be at least h meter tall, they can look up the census and know what they can expect statistically.
If we assume our applicants belong to a uniform distribution; their quality ranges from 0 to 1, we can see that 1) as we have fewer and fewer applicants left in the pool, we must lower our quality acceptance threshold if we seek to maintain the same probability of success, 2) as we hire more and more applicants, we also must lower our quality of acceptance without jeopardizing our chance of success.
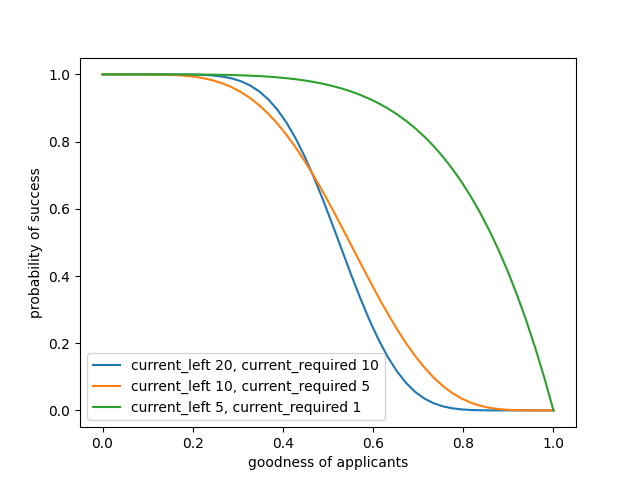
Likewise, we adjust our quality acceptance threshold in the case of a Gaussian distribution. However, what is most interesting is that the bell-shape implies most applicants are average, which implies their quality is on a similar level. This average lowers the probability of success quite dramatically even if we just want push the bar of quality slightly to the right (asking for better).
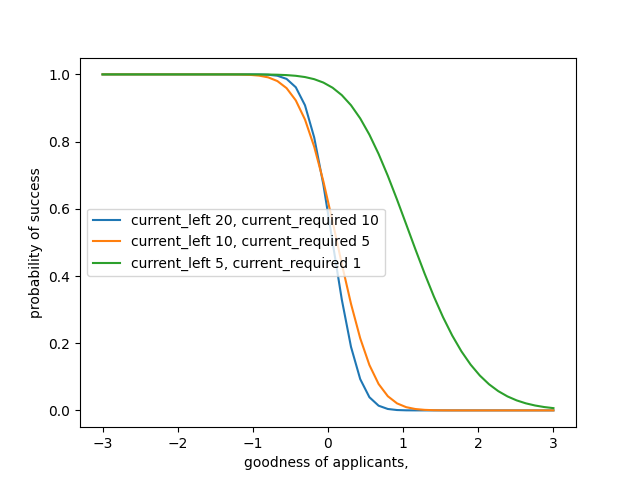
Chapter 2
In chapter 2, the authors explain the difficulty in the trade off between exploration and exploitation. This issue concerns with the problem of when to apply what we know and familiar and when to go outside of our comfort zone and try something new. Let’s loosely define the terms for clarity. Exploration in this context means we try new things and absorb new information that we do not know before or are unfamiliar. Exploitation here means we are making use of our existing knowledge and perform familiar tasks. Often this means we are within our comfort zone. Exploitation and exploration may or may not lead to any good or bad outcome. The problem arises when we can only do either exploration or exploitation.
What to cook tonight? Should we choose to cook what works well in the past or should we cook something that inspires us from the Internet instead?
The authors suggest that we should take the number of chances remaining into consideration. For instance, how many more meals are we going cook for the rest of our lives? Whenever there are many chances left, it may pay to spend more time on exploration at the beginning. Mathematically, one can use a time discount factor to bring the value of the future to present and evaluate the total payoff here and now. The authors highlight this as one possible reason for children, who appear to be curious and lack of concentration, to play and explore more compared to elderly who exploit more in their comfort zone. If we choose exploration, we can apply the optimal stopping to determine how many samples of recipes we need to read about before settling down to try the most appealing so far.
Furthermore, there are times when we have to abandon what we know and explore. For instance, technology that has become obsolete or disruptive change in customer’s preferences. We have learned that in optimal stopping, the more time spent on the look phase, the less time we have for the leap phase. We risk missing out.
The concept of exploration and exploitation slightly relates to the concept of stickiness or inertia. The book mentions a trick. What works may continue to work so we should exploit more of what works. Success has inertia. What fails may continue to fail so we should avoid that and explore other alternatives. In the case of cooking, we should cook the same dish until either its ingredients run out or we hate the dish.
Both exploration and exploitation bring about emotional responses. Exploration may give us excitement, anxiety or regret while exploitation may give us comfort, boredom or regret. One common pitfall the authors warn about is that we often are too slow to explore. For instance, say we bought a packet of 10 of something, we are less likely to explore alternatives until we have consumed all 10 in order to avoid a sense of loss.
Chapter 3
In what order and what comes first (chapter3: Sorting : making order)
Sorting is an important concept in computer science, for sorting is required whenever we want to order a list of objects. The difficulty in ordering things increases with the number of things we have to sort. Scale is the enemy, similar to the optimal stopping problem.
Ordering a list of objects is beneficial if we want to retrieve items in future. The location of an object is known at retrieval time. Ordering a list of objects also makes aesthetic sense. In daily lives, sorting is most ubiquitous during card games, in which we sort our hands such that we will be able to identity advantageous combination quickly. Even though the authors have not gone into great depth on this, one can easily relate sorting to the optimal stopping. After all, we must sort properly in order to determine the best and the worst. During the look and leap phases, we constantly need to sort applicants such that their distribution can be quantified.
This goal of finding the best always come up in sporting competitions. However, there is a caveat. Sport events are designed to entertain rather than to educate the audience on who is the best, second, third, and so on and so forth. Similar level teams are played against another to maximize excitement, but not for accuracy. Thus, it is hard to really place a verdict on which team is better if we take chance into account. Further complicating the outcome is that we may only play the game once and eliminate the loser straight away to save time and expanses and keep the audience entertained. While this is a cost-effective way to generate excitement, its ranking of the best, second, and third may not be a reliable reflection of the team true competence. For instance, the best team is assigned to play against the second best team at Round 1. The second best team loses the game and its chance to play against the third from that moment afterward.
We therefore have to make appropriate trade off between the truth and entertainment. The authors briefly describe a number of classic sorting algorithms. Bubble sort is very robust, but it is very time consuming. It is O(N^2) as it demands pairwise comparisons of every object on the sorting list. Merger sort is very fast. It is O(N * log(N)).
It can be parallelized, a feature that is particularly suitable for a very large data set on computing clusters. It has done so by splitting the list of objects into many shorter chunks. Each chunk is sorted first and later merged to form fewer yet longer lists. The merging part is where we save some effort. Merge until we obtain the full list of sorted objects. While most people do not sort things routinely, one useful idea we could take away from merger sort is merging. It is easier to learn new knowledge if we can absorb new information in small chunk and merge with our prior.
Chapter 4
Caching is the main theme of Chapter 4. Unlike optimal stopping, exploration vs exploitation and sorting, caching is a problem regarding the future, not the present. The difficulty in caching, as explained by the authors, is that in order to know what we should put inside the cache, we need to know what we will retrieve in future. Successful caching requires accurate prediction of future, a very hard task.
Here the authors bring up some typical heuristics that every person can understand and relate to. Before describing what the heuristics are, it is easy to notice many messaging apps automatically order the history of chat messages in a chronological order with the most recent being at the top. Over time, those contacts with which we seldom talk fall to the bottom while those we often talk with rise to the top. Although caching may not be a strictly correct term, the size of the screen is the cache and the list of visible chat history is objects in the cache. Space is precious, for the screen size is extremely limited. Such ordering of chat is to make our lives easier when we need to find and locate chat history that we are interested in. By exploiting our past behaviour, the program makes a straightforward guess that we continue to chat with the same group of individuals. Placing those conversations on top therefore reduces our time to reach for them, unless the assumption of continuation is wrong.
Placing items in chronological order isn’t the only optimal way. But it is very common. For example, news headlines articles, trending search queries. Human memory works on the basis of first in first out whereas logistic warehouses use the basis of first in last out.
Caching has a structural dimension. In the architecture of a CPU such as Intel Core i7 makes heavy use of cache memory. Its L1 is 384KB, L2 1.5MB,L3 12MB. Typically the larger the memory, the more expansive and slower. Thus, caching is a sorting problem in disguise. We aim to sort items by their future importance. We can relate to this in our everyday lives. A firm rents an office in downtown CBD while it rents a warehouse in a suburb. Frequently used items are stored in the office in CBD where most of its employees have readily access. Less frequently used items are kept in the warehouse, maximizing the utilization of rental cost, space and convenience.
Chapter 5
Timing is everything. The authors delineate the tricky aspect of scheduling, mainly dependency. The objective determines the timing. The timing determines the method. The method determines the tools. Scheduling matters. The authors give us three conventional examples. First, if our objective is to reduce wastage, we should eat our earlier grocery first before it expires. Second, if our objective is to reduce latency of our sales representatives, we ought to urge them reply to those customers who raise their questions first. Third, if our objective is to maximize our revenue or income, we ought to schedule our time and energy to tackle the most valuable projects. Fourth, if our objective is to cut down the number of unfinished tasks, we ought to start completing those easy and short ones.
Not all tasks are created equal. The book highlights the conventional wisdom that we can assign any task to one of four quadrants. The first quadrant contains tasks that are important and urgent. The second contains tasks that are important but not urgent. The third contains tasks that are unimportant but urgent. The last contains tasks that are unimportant and not urgent. The authors caution us that what may first seem unimportant can be significant whenever they are required to be completed before others.
To help with organization, we use a Gantt Chart. The chart provides a visual representation of dependency and chronological order. Parallelized tasks show up on different rows that overlap with one another. The nuance the authors pay attention to is the trade off between throughput and delays. Apparently, what we think of parallelized tasks may not be truly parallelized and switching between them incurs friction. Using an example of OS scheduling, the authors explain that users experience the impact of high latency of various applications by switching amongst them frequently. This incurs switching cost and the computing throughputs overall drops. In the real word, we often pay the switching cost whenever we change from one task to the next. For example, replying messages or interruption while programming a module or writing an article is inefficient.
Switching brings about hidden burden. We see it and know it as we have to re-focus our mind on the task at hand after coming back to it from somewhere else. Hence, a good schedule ought to offer a block of undisrupted time to get things done without costing too much delays. Of course, a Gannt Chart also offers much more that are beyond the scope of this chapter. Unfortunately, life can throw us new surprises that render old plan irrelevant and obsolete.
Chapter 6
Uncertainty comes into the mind of decision making in When should we change our mind (chapter6: Bayes’s Rule : predicting the future). If you want to estimate the probability of the chances of your bus arriving on time at a bus stop, one simple heuristics is to sum up the number of past incidents plus one and divided by the total number of the bus arriving at the stop plus two.
The intuition behind this heuristics is that when the event is frequent, we converge to the true underlying probability, and that when the event is rare, we converge to 50-50.
In this chapter, the authors highlight several essential concepts in Bayesian statistics. The concept of prior distribution is the information or knowledge we have known already. This prior can be wrong, but that is what we have got without further updates. Unlike prior distribution, the concept of posterior distribution is knowledge gained when new information arrives or something else has occurred.
The crux of the prediction boils down to how we could best update and improve our prior and posterior distributions to describe reality. The authors suggest a simple 4-step procedure. First, let our goal be as ambitious as predicting the future, but we ought to accept our prediction to have a wide range. Second, let’s make a preliminary prediction from our prior knowledge. Third, stream the latest information to adjust our prior knowledge if our prediction is inaccurate. Yet, the prior could still be inaccurate even if the prediction is right. Fourth, update the posterior as new information arrives.
The hardest part of predicting the future is that there are many factors leading to an outcome. To disentangle these factors, the authors emphasize the key difference between association and causation. Association refers to two variables occur at the same time but one DOES not cause the other to happen. One variable does not come into existence and has nothing to do with the lack of the other variable. On the contrary, causation means one variable causes another variable to either disappear or appear. The relationship means that you must have one before the other. For example, polar bear and ice. A polar bear does not make ice. Ice does not make a polar bear. However, they are associated together because of the ecosystem and habitat. Thus, polar bear and ice is association, not causation.
When it comes to distributions, their shape matters. Here the book introduces three typical distributions, namely normal, power-law and Erlang distributions.
The normal distribution is fat at the center at the average and symmetrical on both sides. So, as a rule of thumb, we should always predict the sample average if our prior knowledge tells us whatever we are dealing with comes from a normal distribution.
The power-law distribution is long-tailed. So, as a rule of thumb, we should always predict the lower end of the value range for a sample. However, as the sample creeps to the right, our prediction should be scaled multiplicatively. For instance, doubling the box office if a movie keeps staying on the top view counts. As an aside, the frequency of occurrence of English words is described by Zipf’s law, which is similar to the power-law distribution.
The shape of Erlang distribution is like the mixing of the normal and power-law distributions. So, as a rule of thumb, we can be safe to play with the median. However, as new information arrives, we could adjust our prediction by scaling it additively. For example, we add another 10 minutes to the wait whenever our bus is late.
Chapter 7
Over-fitting is a common problem faced by computer scientists who heavily use mathematically modelling to describe real world processes. In this crucial chapter, the authors try to use polynomials or mathematical constructs to describe and explain how this problem arises and how to solve it. I seek to differ and try to offer a very simplistic way to delineate the basic idea to the public at the risk of the loss of accuracy.
I think the quote “Never Attribute to Malice That Which Is Adequately Explained by Stupidity” adequately and eloquently summarizes this key idea behind over-fitting.
Let me unravel the quote a little bit deeper. The assumption behind the quote, in my opinion is that stupidity is far more likely and far more common than malice, a state of affair that is good for the world generally. Malice, if done properly, requires dedication, preparation, intelligence, timing, skills and luck. Successful malice is thus far less likely than stupidity which requires none of the above. When in doubt, choose whatever simpler and more common.
In contrast, when should we choose malice? One should choose malice when it is too hard to explain with stupidity alone. For instance, if the rationale centers around a complicated combinations of stupidity, carelessness, absentmindedness, forgetfulness, lack of information, Force Majeure. Then, malice is the simpler and more likely option as stupidity at extreme level is indeed quite rare.
With this basic idea in mind, we can return to our attention on model construction and development. The authors suggest we should run some tests to validate our prior knowledge about the world and update it as described in earlier chapters. The whole point of this exercise is to bring the knowledge closer to reality. Some negative examples include students who are good at sitting examinations but poor at solving life problems. During their course of study, their prior knowledge has been moulded closer to what is expected of them by examination system and farther away from the real world.
In addition to describing this problem of overfitting, the authors make some suggestions on how to detect and contain it. The detection method is called cross-validation. The concept of cross-validation is to test as we learn. First, we split our problems into two parts. One for learning; another for validation. We learn the material only from the learning set and we test our knowledge on the validation set to check how accurate our learning has been. To check means we complete some assignments during both learning and validation and are evaluated against some metrics or scores. If our learning score is higher than validation scores, our learning have overfitted. If our learning score is lower than validation scores, we have cheated. If both scores are similar, we are okay.
Last but not least, it is better to spend more time and energy to contemplate causality and less on association, a key concept we have already discussed at length previously. Thus, we should down-weight our experience, keep a keen eye on survivorship bias, and be especially vigilant as we face the ebb and flow.
Chapter 8
The key takeaway of Relaxation : let it slide is to abstain from binary thinking. One easy trap we fall into is to think about the world as binary. We might think about what interest we pursuit if we have won a lottery. We might also think about what we do to make a living. However, we seldom manage to find a solution that fits our passion and livelihood.
The immediate implication is that often people choose either livelihood or passion. The gap between these two activities at first sight leads most people to fail to optimize for the better. The authors suggest that there is a better way. A compromise. We should make a compromise between our passion and livelihood. In order to find and evaluate a compromise, we must explore and rank various alternatives. The skills required to do so have already been introduced in earlier chapters.
Chapter 9
Randomness : when to leave it to chance. The title of this chapter encapsulates its essence. Although the word chance may suggest something outside of our control, the actual meaning in this case is well within our control. When we say chance, we are trying to express our inability to fully comprehend a population. Thus, we resort to sampling as a strategy to gain a faithful estimate of the entire population statistically without explicitly looking at every member of a population. Sampling depends on the underlying distribution at least in theory. However, due to the occurrence of chance and randomness, there is NO guarantee that our collected samples are representative and portray the real distribution; we therefore describe such uncertainty by statistical measures such as standard errors and averages.
Apart from our inability to fully comprehend a population, there are other circumstances in which sampling is beneficial or even is the sole option. Sampling can be used in place of analytical thinking when thinking is slow and expansive while sampling is fast and cheap. For instance, it is far easier and cheaper to look up the pay scale of software engineers on a job hunting website than to analyze a company’s financial health, the contribution of software component to its services and products, and individual’s competency and productivity.
Prime number and its unique usage in cryptography employs sampling. Prime numbers when multiplied by some special numbers yield number with some characteristics. However, this behaviour is not always true. Thus, the pragmatic solution is to perform a series of multiplication to test the number of its likelihood of being a prime number, during which each step allows for some acceptable false alarm rate. Longer the test series, higher our confidence on weather or not the number is a prime.
Outside of mathematics, biology, sociology and many other disciplines rely on sampling heavily. One reason, I suspect, is that it is hard to pinpoint causal relationships in problems concerned by scientists of those disciplines and to conduct controlled experiments. Rather than observing causal relationships, they observe complex interactions and associations. However, sampling is no panacea. Sampling is unsuitable for things that rarely occur. Some infamous examples include Great Depression, 100-year flood, etc.
With all that information, we close the section on man versus nature. All the previous chapters try to illustrate what individuals reactions or responses are in light of the insights from computational algorithms. Nature does not second-guess man and does not respond to our actions in anticipation of our actions. The upcoming two chapters explore the thinking of computer scientists on man versus society, in which our actions bring about the reactions of others which in turn bring about our reactions.
Chapter 10
The chapter centers on how computers or devices really connected together to form the so-called the Internet. This is particularly interesting because one key concept emerges from the work of the Internet is the development of a protocol. In short, a computer talks to another computer in ways that are radically different from human interactions. A computer uses many-to-many node interactions. The same message can be copied and distributed on the network simultaneously. The message is chopped up into smaller packages and are sent out to the network. Since there are so many computers working in the network, the arrival or departure of packages appear to be random and unpredictable.
With that in mind, our solution must entail the following attributes in order to cope with the demand characteristics of the internet. First, the network has to be robust and reliable. Obviously, it needs to serve billions of users daily. Second, the network has to be able to handle randomness, a circumstance that is very tricky for a scheduler (please refer back to the scheduling chapter for a more in-depth discussion). Third, the network has to be distributed, not centralized.
If we want to circumvent the need for the creation of a centralized party that uses a top-down approach to mange the entire network, we must establish a bottom-up approach in which everyone obeys some agreed-upon protocol. If we want to increase the robustness and reliability of the network, we must recognize that there will always be mistakes when we pass along package of messages, and we must tolerate some errors. Thus, the solution enforces that the same messages are to be duplicated, split up into many smaller pieces, and sent to the destination via many different routes simultaneously. Often the shortest route may not be the fastest due to traffic congestion at the network nodes along the path. From one node to the next, we check the next node has actually gotten the message by asking for a confirmation message. When this confirmation is performed every time, the traffic volume easily doubles as a result. Yet, this confirmation ensures us if a packet is lost, we know about the loss and can resend the missing package.
Today, TCP is the protocol that underpins the entire Internet as we know it. One rule I find most interesting is the rule on backing off. The rule has two parts. When the rate of sending and receiving confirmation is fast, the rule says we should gradually ramp up the rate of sending incrementally. When the rate of sending and receiving confirmation is slow and coming to a halt, we should then back off rapidly. It is asymmetrical. For instance, when our browser fails to fetch a website, we first retry after 2 minutes, then 4, 8 and so on. The retry wait duration grows multiplicatively longer. Thus, it is interesting that the saw-toothed shape of traffic flow is indeed the most optimal on average for everyone as a whole.
Here, we can relate to the concept of delays and throughput from earlier chapters. The node of the network and us (users) face the dilemma of delays and throughput just like a resource scheduler. A node is just like a computer with limited resources. Lower delay means the node puts priority on incoming signals whenever they arrive by switching to them. However, as we have seen earlier about switching cost and protocol, these signals can often be randomly distributed and in small pieces. Processing them as they come by increases switching cost but reduces delay at the expense of lower throughput. Thus, one design feature of nodes is a buffer or queue. A queue allows us to put tasks on hold until earlier tasks are completed. This helps keep switching cost low and throughput high. One draw-down is that when the queue grows too long, the delay becomes too noticeable for users.
Another point worth mentioning is the importance of each message. As in resource scheduling, we need to give a score of priority for each task. As the traffic slows with growing number of users on the Internet, it is imperative to prioritizes the most important messages. One feasible solution is to kick out messages once the queue grows too long. In doing so, users would have to resend the same message again when it fails earlier. Yet, this very act of resending broadcasts to the network that this is important. Also, kicking messages out automatically keeps delays low and traffic less congested. So long as we can ensure the message is resent by the user who really wants to do that, instead of by some automatic software.
##Chapter 11 Game theory : the minds of others is an introductory chapter on game theory and not much on algorithms. It briefly sheds lights on how game theory works but leaves out algorithms.
For those who are interested in learning more about algorithmic game theory, the interface of theoretical computer science and game theory, would have been sorely disappointed.
I did a quick search on algorithmic game theory; what I quickly realize is that algorithmic game theory is a complex subject, despite of its young age. Someone even wrote an entire book called [Algorithmic Game Theory] (https://doi.org/10.1017/CBO9780511800481).
The first dilemma is the prisoner’s dilemma, a classic problem in game theory. The crux of the dilemma is how to act when you cannot be sure of what the other person may do in response to your action. And their reaction inevitable impacts on your gain or loss. This invites recursive guesses. Both parties guess the mind of another and act according to what they believe to be in the best interests for themselves. Hence, we strive to maximize our gain and minimize adverse consequences of other’s actions.
Mind games are tiresome. Is there a situation in which we no longer need to care about what the other person may act? Is there a situation in which everyone is acting most optimally and remains so permanently? Theoretically, this situation is known as Nash equilibrium. One example is a stalemate in chess. Neither player can win nor lose. From this, we can see that Nash equilibrium only means the player’s actions remain constant, but it does not mean that players are better off or worse off. One caveat of Nash equilibrium is that we have no way of knowing how to guarantee players can reach there.
Prisoner’s dilemma is two people game. Prisoner A and B. They are identical in all imaginable aspects, including what they can do. They can either confess or remain in silence. With two options, we have four outcomes, each with a different payoff for the prisoners. If both confess, both serve 5 years in prison. If either one confesses and the other remains silent, the one who confess is set free and the one who remains silent serve 20 years. If both remain silent, they serve only 1 year in prison.
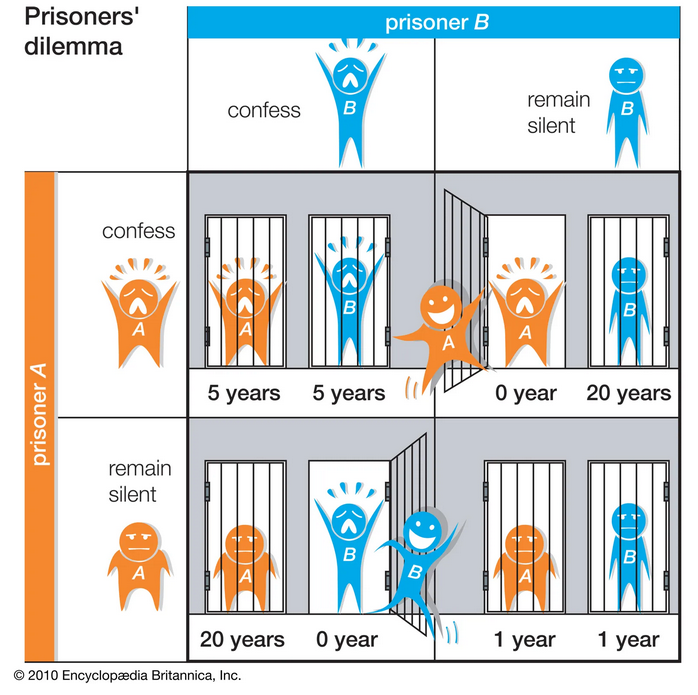
From the point of the prisoners, it appears that they would like to serve only 1 year in prison and therefore say nothing. However, not knowing whether or not the other prisoner would confess, the prisoner’s best move is always to confess. Thus, the outcome is that both serve 5 years in prison. Thus, we can use this insight to explain why ethics and brotherhood is highly regraded as this introduces a penalty to confessors.
Another problem is the tragedy of the common. The most intriguing observation is that when everyone does the same action, the advantage it brings over others disappears. Some classic examples are warfare and price war. Any effort spends on improving its competitive advantage is cancelled out on net.
The US labor market provides an interesting real life illustration of the tragedy of the common. American workers are entitled to annual leaves. On average, workers take 50% of their annual leaves. 15% of them takes no leaves. The motivation at first seems contradictory. Why workers would not want to take as many days off as possible given that the law enables them to do so?
One possible explanation provided by game theory is that when a worker takes more days off than his colleagues, he appears to be a lazy, unmotivated, and unambiguous fellow, inflicting damages on his image in the eye of his superior and his chance of a promotion. Thus, the outcome is that he would like to take one day fewer than his colleague.
The chapter ends with a very brief discussion of the various types of auctions. However, auctions are far more complicated and deserve many more lengthy paragraphs, so we shall leave the chapter with my final remark: if you are unsuited for the game you are playing, then quit and don’t play that game. In other words, if you are the mouse in a cat and mouse game, don’t play that game.
Conclusion
In this concluding chapter, the authors point out the ubiquitous fact that a programmer like myself can easily identified with: thinking in algorithmic terms is no easy task. The task is laborious, tiresome and enervating. The authors believe it is compassionate to let people think less, not more. How, perhaps one can seek help from artificial intelligence.
P. S.
For those who would like to explore this topic more, here is my recommendation. Written by Daniel Kahneman, a co-recipient of the Nobel Prize for Economics in 2002 , Thinking fast and slow is a book about how we think, process information and decide.
